Question

100 баллов! Помогите, пожалуйста! 3 и 4 задача. Очень прошу вас! Третью с чертежом, молю!
Желательно обе задачи, но можно одну в крайнем случае! Только верное и понятное решение, пожалуйста! ​

Answer 1

Ответ:

Вписанный четырехугольник.

Answer 2

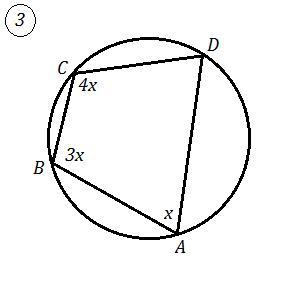
3)   Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°.

Так как углы, взятые в порядке следования относятся как 1:3:4 , то ∠А=х , ∠В=3х , ∠С=4х  и  ∠А+∠С=х+4х=5х=180°  ,  х=36° .

∠А=36°  ,  ∠В=3*36°=108°  ,  ∠С=4*36°=144°

Сумма внутренних углов четырёхугольника равна 360°.

∠D=360°-36°-108°-144°=72°

Или  ∠В+∠D=5х  ,  ∠D=5x-∠B=3x-3x=2x  ,  2x=2*36°=72° .

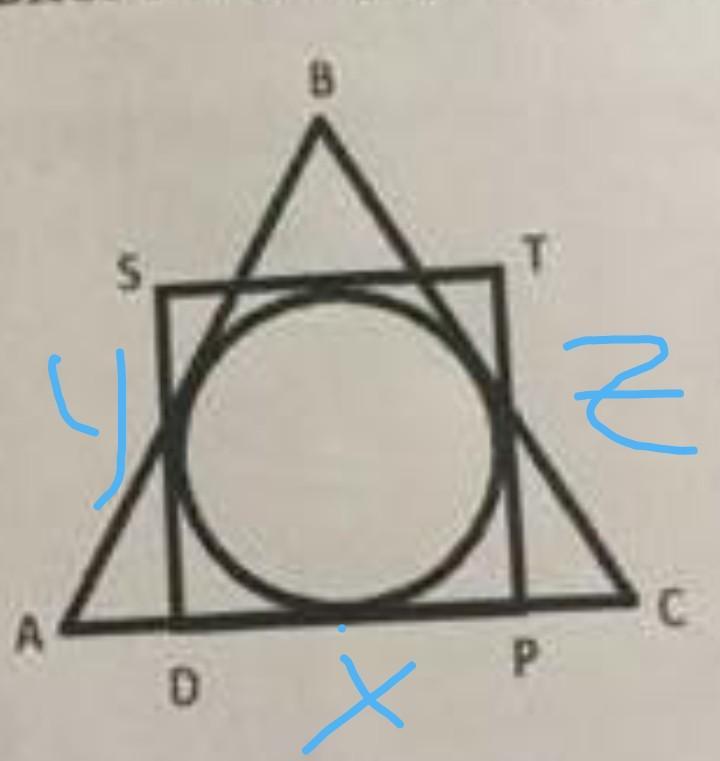
4)  Сторона правильного треугольника равна  $a=3\sqrt6$ .

Радиус вписанной окружности в прав. тр-к  равна 1/3 его высоты, то есть  $r=\frac{1}{3}\cdot \sqrt{a^2-(\frac{a}{2})^2}=\frac{1}{3}\sqrt{\frac{3a^2}{4}}=\frac{1}{3}\cdot \frac{a\sqrt3}{2}=\frac{a\sqrt3}{6}$  .

Сторона прав.четырёхугольника - квадрата, описанного около окружности, равна   $b=2r=2\cdot \frac{a\sqrt3}{6}=\frac{a\sqrt3}{3}$  .

Периметр квадрата равен  $P=4b=4\cdot \frac{a\sqrt3}{3}=4\cdot \frac{3\sqrt6\cdot \sqrt3}{3}=4\cdot \sqrt{18}=12\sqrt2}$  см.