Предмет: Алгебра,
автор: Fishtooth
Решить уравнение, 100 баллов
Приложения:
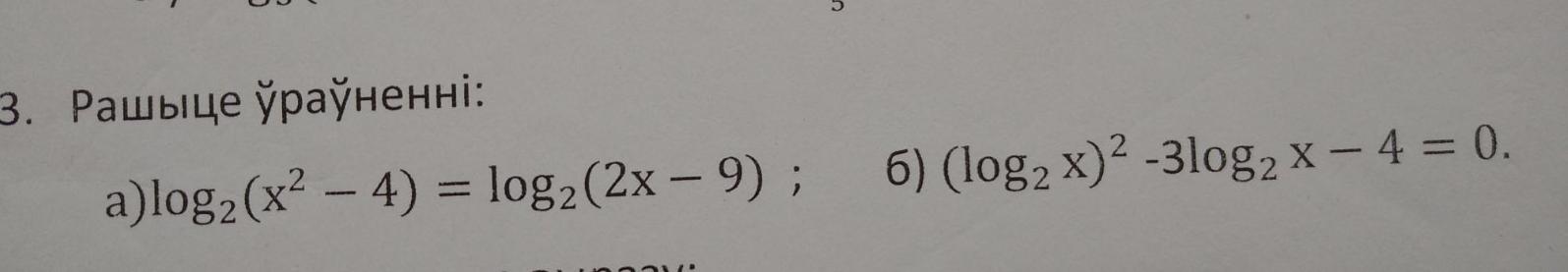
Ответы
Автор ответа:
1
Ответ:
(см. объяснение)
Объяснение:
1)
Уравнение несложное, даже не на логарифмы.
Просто просчитаем ОДЗ:
А теперь решим:
Тогда ответ: нет корней.
2)
Здесь ОДЗ x>0.
Тогда:
Теперь рассматриваем 2 случая:
С учетом ОДЗ посторонних корней нет.
Похожие вопросы
Предмет: Русский язык,
автор: hibarisempay
Предмет: Русский язык,
автор: hibarisempay
Предмет: Русский язык,
автор: sasha14080898
Предмет: Математика,
автор: Человек8877
Предмет: Математика,
автор: Человек8877