Дифференциальные уравнения. Задание на фото
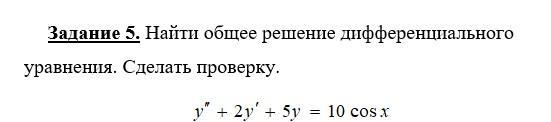
Ответы
Ответ:
y(x)=Yc(x)+Yp(x)=2cosx+sinx+c₁e⁻ˣcos2x+c₂e⁻ˣsin2x
Пошаговое объяснение:
так вроде.
но я хз, давно их не решала.
y''+2y'+5y=10cosx
d²y(x)/dx²+2*dy(x)/dx+5y(x)=0
y(x)=e^(λx)
d²/dx²(e^(λx))+2d/dx*(e^(λx))+5*e^(λx)=0
λ²e^(λx)+2λe^(λx)+5e^(λx)=0
(λ²+2λ+5)e^(λx)=0
λ²+2λ+5=0
λ=-1+2i or λ=-1-2i
y₁(x)=c₁e^((-1+2i)x)
y₂(x)=c₂e^((-1-2i)x)
y(x)=y₁(x)+y₂(x)=c₁e^((-1+2i)x)+c₂e^((-1-2i)x)
e^(α+iβ)=e^α*cosβ+ie^α*sinβ
y(x)=c₁(e⁻ˣcos2x+ie⁻ˣsin2x)+c₂(e⁻ˣcos2x-ie⁻ˣsin2x)
y(x)=(c₁+c₂)e⁻ˣcos2x+(c₁-c₂)e⁻ˣsin2x
Yp(x)=a₁cos+a₂sinx
dYp(x)/dx=d/dx(a₁cos+a₂sinx)=-a₁sinx+a₂cosx
d²Yp(x)/dx²=d²/dx²(a₁cos+a₂sinx)=-a₁cosx-a₂sinx
d²Yp(x)/dx²+2dYp(x)/dx+5Yp(x)=10cosx
-a₁cosx-a₂sinx+2(-a₁sinx-a₂cosx)+5(a₁cos+a₂sinx)=10cosx
(4a₁+2a₂)cosx+(-2a₁+4a₂)sinx=10cosx
4a₁+2a₂=10
-2a₁+4a₂=0
a₁=2
a₂=1
Yp(x)=2cosx+sinx
y(x)=Yc(x)+Yp(x)=2cosx+sinx+c₁e⁻ˣcos2x+c₂e⁻ˣsin2x