Предмет: Алгебра,
автор: BurganoiD
Помогите пожалуйста решить показательные неравенства
Приложения:
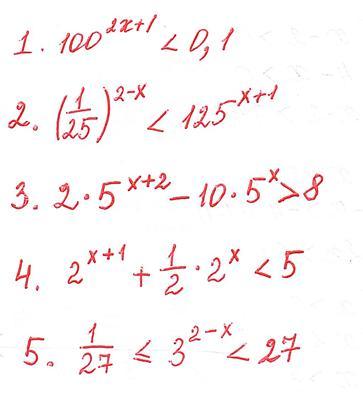
Ответы
Автор ответа:
1
1)
2)
3)
4)
5)
Автор ответа:
2
Х<-3/4
Х>-7
Х>-1
Х<1
Х=-1
Приложения:
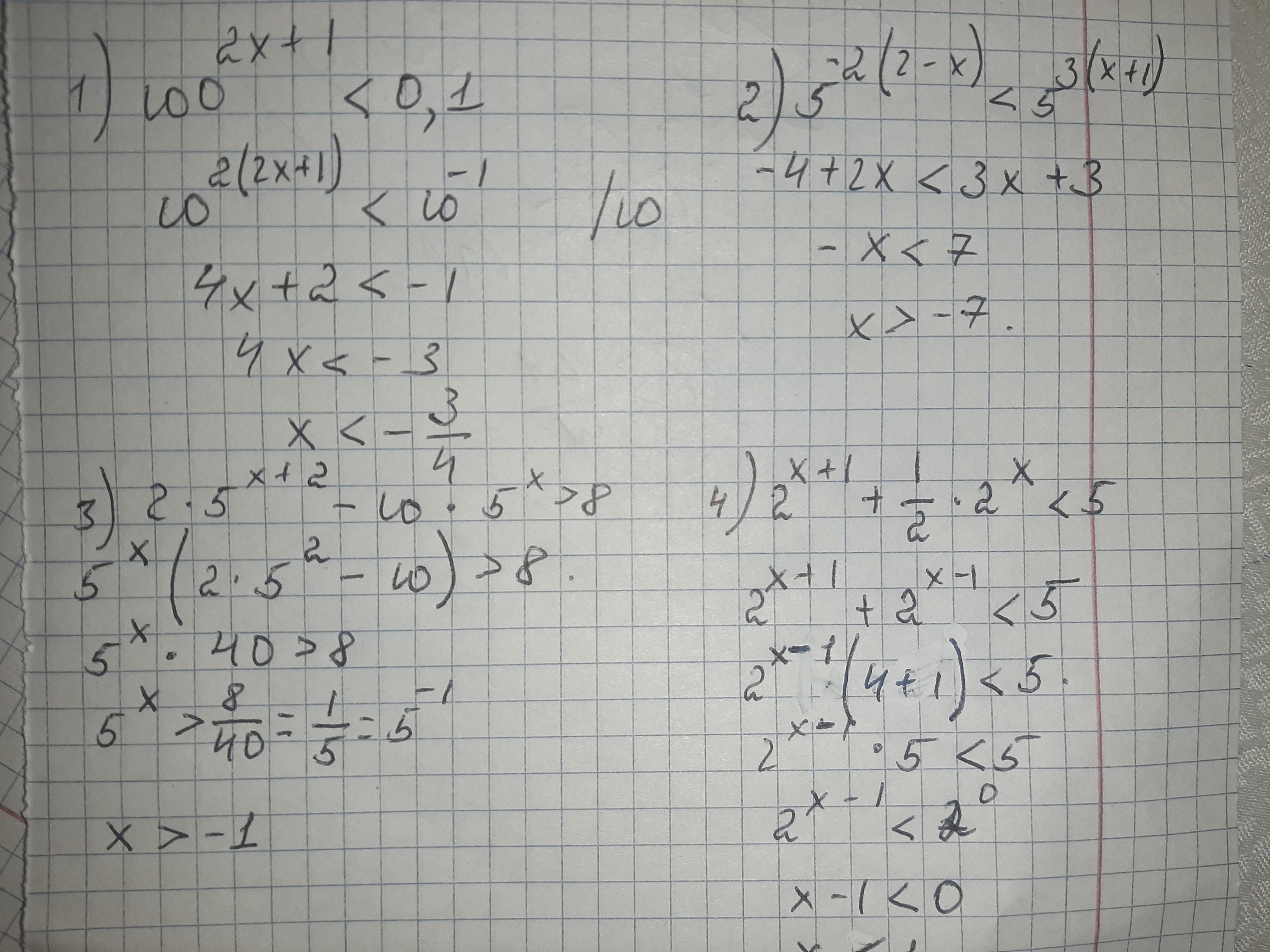
Похожие вопросы
Предмет: Русский язык,
автор: anfisa2003
Предмет: Русский язык,
автор: Artik12312
Предмет: Английский язык,
автор: Vorozheinaluba
Предмет: Алгебра,
автор: alinakam
Предмет: Математика,
автор: asadulaeva2003