Question

Все ученики старших классов (с 9-го по 11-й) участво­вали в
школьной спартакиаде. По результатам соревнований каждый из них получил
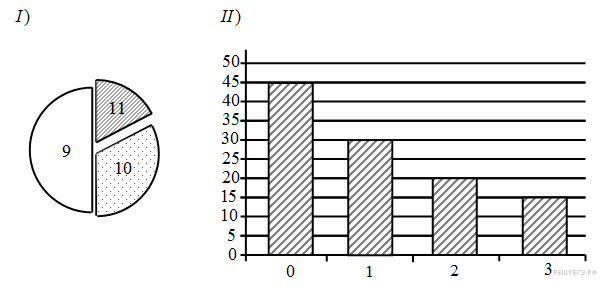
от 0 до 3-х баллов. На диаграмме I отражено распределение учеников по
клас­сам, а на диаграмме II — количество учеников, набравших бал­лы от 0
до 3-х. На обеих диаграммах каждый ученик учтён толь­ко один раз. 
 
Имеются четыре утверждения: 

1 ) Среди учеников 9-го класса есть хотя бы один, набравший 2 или 3 балла. 
2 ) Все ученики, набравшие 0 баллов, могут быть 9-классниками. 
3 ) Все 10-классники могли набрать ровно по 2 балла. 
4 ) Среди набравших 3 балла нет ни одного 10-классника. 
Какое из этих утверждений следует из анализа обеих диа­грамм?

Answer 1

1) Не верно!
Общее количество учеников равно:
45+30+20+15=110
Из диаграммы видно, что на долю учеников 9-го класса приходится ровно половина, значит:
110/2=55 - количество учеников 9-го класса.
Предположим, что всю долю учеников, получивших 0 баллов составляет 9-ый класс, тогда:
55-45=10 - учеников, которые точно не могли получить 0 баллов. Все эти 10 учеников могли получить 1 балл, значит, утверждение ложно.
2) Верно!
Опять же, на долю учеников 9-го класса приходится 55 человек, а получило 0 баллов  45, значит всю долю получивших 0 баллов, может составить аудитория 9-х классов
3) Не верно!
Половина от всей аудитории равна 55, а четверть примерно равна 28. Аудитория 10-х классов составляет больше четверти всей аудитории, следовательно, их число немного превышает 28. Между тем, 2 балла получило лишь 20 человек, следовательно, весь 10 класс не могу получить 2 балла
4)Не верно!
(Опираюсь на то, что это не предпологается, а утверждается)
Опять же на долю 10-классников приходится больше 28 человек. Доля учеников, получивших 3 балла:
15/110*100~=13%
Если разделить на 4 части(2 части составляет 9 класс), то получим примерно 3%. Получается, в среднем, от количества 10-классников примерно 4%(Их больше 1 части).Следовательно, нельзя точно(именно точно) утверждать, что таких учеников нет.