Предмет: Алгебра,
автор: universale2012
Примеры по алгебре для задание положительными и отрицательными степенями
ОБЪЯСНИТЕ, как их делать.
Приложения:
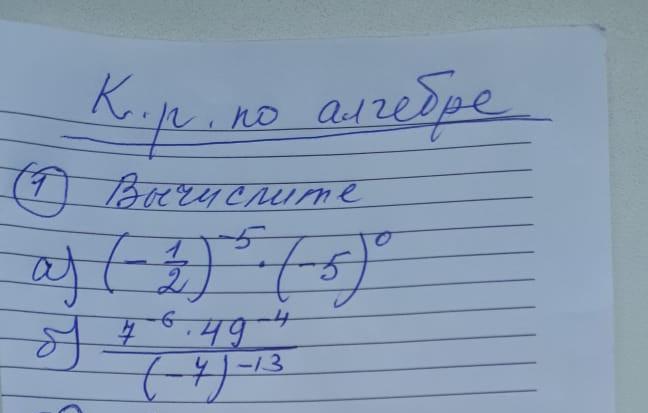
Ответы
Автор ответа:
1
universale2012:
Я не ругаю, просто спрашиваю: вот в первом.мы записали сам пример ты ставишь равно. вопрос откуда у тебя (-2), появилось ведь дробь 1/2= 0.5 или как?
А откуда (- 2) у того, кому отметили "лучший ответ" ? Поругайте его и спросите у него же .
Выплёскивайте свой гнев где-то в другом месте, а не на этом сайте.
К Вам мой гнев не имеет никакого . А вот когда стараешься кому- то помочь и решаешь задание, а вместо спасибо человек, ничего не смыслящий в математике, готов тебя поругать непонятно за что, вот тогда невольно разгневаешься.
Никакого отношения
Уважаемый, Universalka. В вопросе я попросил объяснить: как на что надо делать и что делать. Frizon прикрепил не только решение, но и объяснил что и зачем.
Автор ответа:
2
Ответ:
а)
Первую часть "переворачиваем", чтобы степень стала положительной. Любое число в степени 0 равно 1.
б)
Степень в степени умножаются. Далее степени с одинаковыми основами прибавляются. Потом снова "переворачиваем" дробь, чтобы степень стала положительной. При делении степений мы их отнимаем.
В первом задании ответ - 32 , а не 32 .
Опечатался, спасибо.
"При делении степений мы их отнимаем." Кого их ?
Степени, очевидно.
Не степени, а показатели степеней, очевидно.
Похожие вопросы
Предмет: Русский язык,
автор: rinaabysheva
Предмет: Русский язык,
автор: princesa55
Предмет: Русский язык,
автор: aleksxamaty
Предмет: Алгебра,
автор: gun6
Предмет: Геометрия,
автор: Arista666