Предмет: Алгебра,
автор: sallyhoffman
Неопределённый интеграл
Приложения:
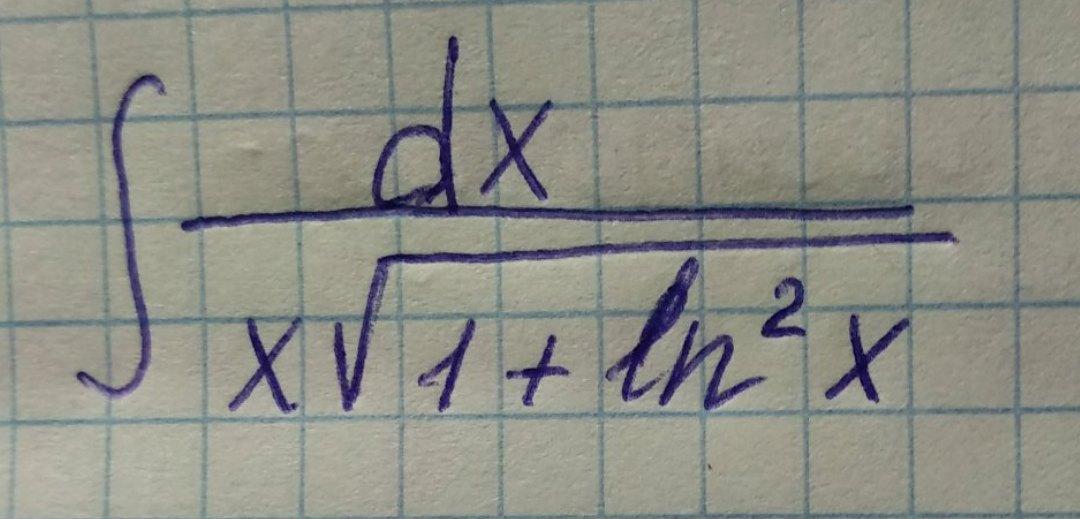
Ответы
Автор ответа:
0
Автор ответа:
0
Подведем логарифм под знак дифференциала, поскольку
d(㏑x)=dx/х, напомню, что дифференциал функции - это произведение дифференциала аргумента х на производную
(㏑x)'=1/x, поэтому уместна замена ㏑х=у, тогда интеграл приобретет вид табличного т.е. ∫dx/(x*㏑x)=∫d(㏑x)/√(1+㏑²x)=
∫dу/√(1+y²)=㏑Iy+√(1+y²)I+с=㏑I㏑x+√(1+㏑²x)I+с
Похожие вопросы
Предмет: Русский язык,
автор: gaybiza
Предмет: Русский язык,
автор: Енонок
Предмет: Английский язык,
автор: 626626
Предмет: Алгебра,
автор: megacat2
Предмет: Химия,
автор: TheBester236