Предмет: Алгебра,
автор: russia666999
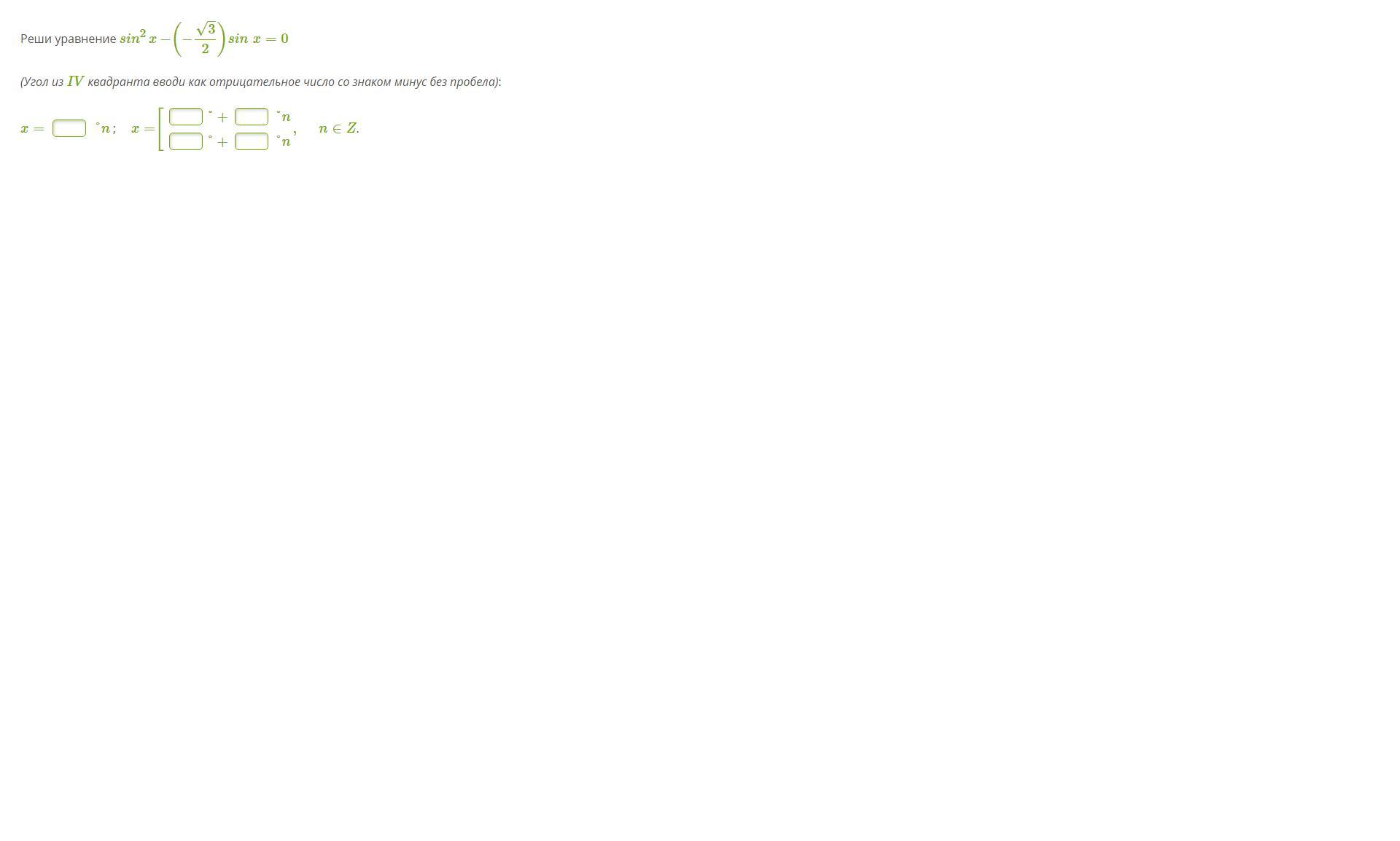
Решите пожалуйста задание
Приложения:
Ответы
Автор ответа:
2
Получаем совокупность уравнений:
Похожие вопросы
Предмет: Английский язык,
автор: kamilq40
Предмет: Русский язык,
автор: ксенька2005
Предмет: Русский язык,
автор: Подруженции2507
Предмет: Математика,
автор: Аноним