Предмет: Математика,
автор: GergalovStanislav
Помогите решить (п.с. поподробнее, почему такой вариант ответа и график функции, если можно):
Приложения:

sergyzak2020bor:
у квадратичной функции 3 (ТРИ нуля????!!!) как? вертайте мое решение. верно там все
нули тут х=0 и х = -10, там не куб, а квадрат f(x)=x^2+10x = х(х+10)
Ответы
Автор ответа:
1
Ответ:
4) минимум = -25
Пошаговое объяснение:
нули функции f(x) = x^2+10x = x(x+10) = 0 при x1 = 0, х2 = -10
квадратичная парабола, роги вверх,
отрицательные значения - промежуток между корнями (нули)
1) квадратичная парабола. максимум нулей =2
2) 6>0 - функция возрастает
3) максимума нет (роги вверх)
4) верно. минимум пр f'(x) = 0; f'(x) = 2x +10 = 0 ; x = -5 ; f(-5) = -25
5) f(f(1)+1) = f(12) 12 - не ноль и на -10 - явно не 0
6) x > 10 - функция положительна
7) квадратичная парабола не симметрична оси 0х никогда
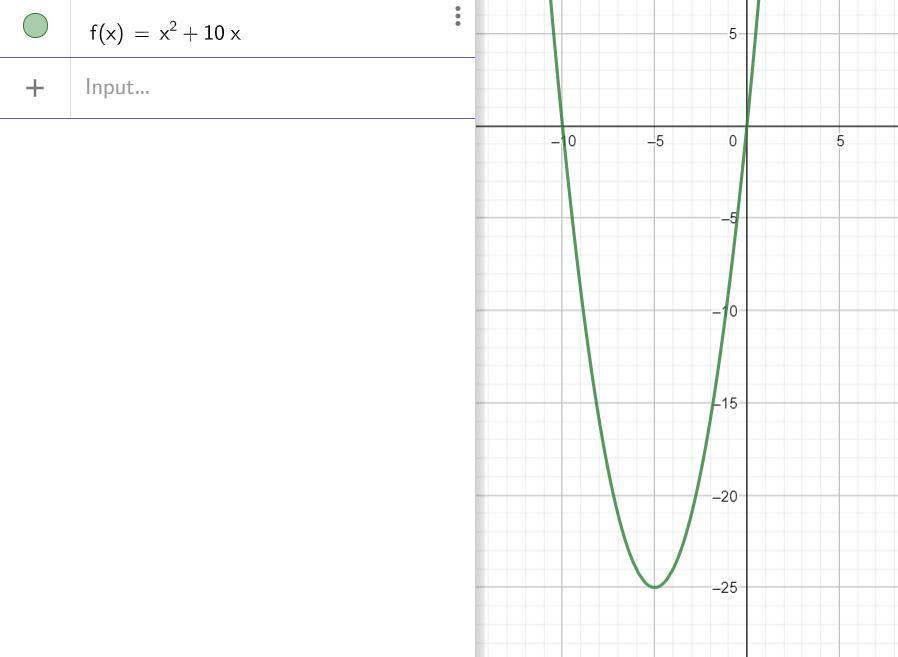
график прилагается
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: eleershowa
Предмет: Русский язык,
автор: a09
Предмет: Русский язык,
автор: Lusi62
Предмет: Математика,
автор: AnyaTyanNya
Предмет: Алгебра,
автор: MarySestra