Question

осевое сечение конуса - правильный треугольник, вокруг конуса описана
сфера. Найдите ее площадь, если радиус основания конуса равен 2√3 см

Answer 1

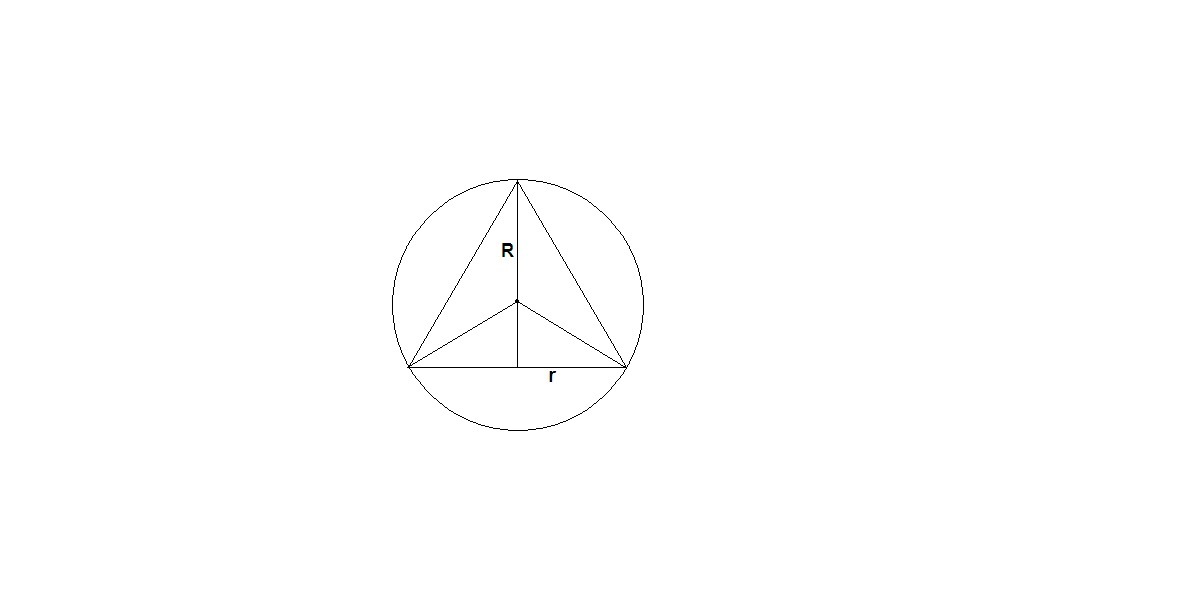
Если провести осевое сечение конуса, то получим правильный треугольник, вписанный в окружность - сечение сферы, проходящее через ее центр.

Значит радиус окружности, описанной около правильного треугольника и есть радиус сферы:

R = a√3/3

а - сторона правильного треугольника, она равна диаметру основания конуса:

а = 2r = 2 · 2√3 = 4√3

R = 4√3 · √3 / 3 = 4

Площадь сферы:

S = 4πR² = 4π · 4² = 64π кв. ед.