Question

СРООООЧНО ДАМ 50 БАЛЛОВ ПОМОГИТЕ РЕШИТЬ ХОТЬ ЧТО НИБУДЬ​

Answer 1

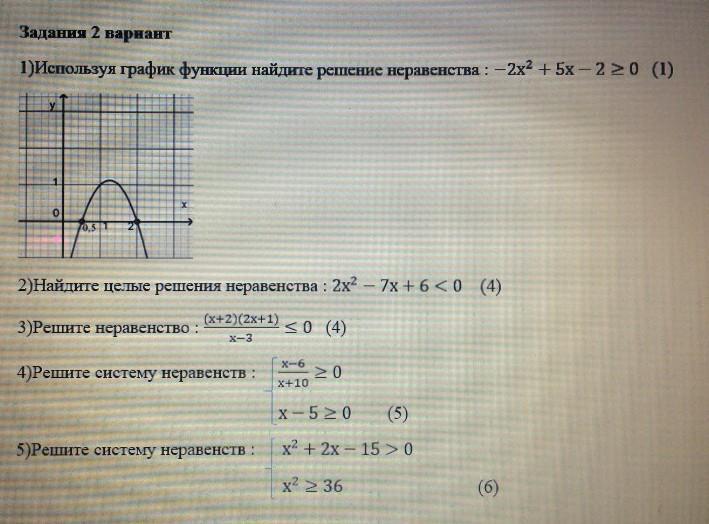
1. На графике решение неравенства - это часть параболы, которая находится на прямой y = 0 (ось OX) и выше неё.

$x\in[0,5;\;2]$

$2.\;2x^2-7x+6<0\\2x^2-7x+6=0\\D=(-7)^2-4\cdot2\cdot6=49-48=1\\x_{1,2}=\frac{7\pm1}4\\x_1=1\frac12,\;x_2=2\\\\(x-1\frac12)(x-4)<0\\x\in(-\infty;\;1\frac12):\;\;(x-1\frac12)(x-4)>0\\x\in(-1\frac12;\;4):\;\;(x-1\frac12)(x-4)<0\\x\in(4;\;+\infty):\;\;(x-1\frac12)(x-4)>0$

Ответ: $x\in(1\frac12;\;4)$

$3.\;\frac{(x+2)(2x+1)}{x-3}\leq0$

О.Д.З.:

$x-3\neq0\\x\neq3$

Решение:

$\frac{2(x+2)(x+\frac12)}{x-3}\leq0$

В точках $-\frac12$ и -2 выражение обращается в 0. Определим значение выражения на интервалах (не забываем об О.Д.З.)

$x\in(-\infty;\;-2]:\;\;\frac{2(x+2)(x+\frac12)}{x-3}\leq0\\\\x\in(-2;\;-\frac12):\;\;\frac{2(x+2)(x+\frac12)}{x-3}>0\\\\x\in[-\frac12;\;3):\;\;\frac{2(x+2)(x+\frac12)}{x-3}\leq0\\\\x\in(3;\;+\infty):\;\;\frac{2(x+2)(x+\frac12)}{x-3}>0$

Ответ: $x\in(-\infty;\;-2]\cup[-\frac12;\;3)$

$4.\\\begin{cases}\frac{x-6}{x+10}\geq0\\x-5\geq0\end{cases}\Rightarrow\begin{cases}\frac{x-6}{x+10}\geq0\\x\neq-10\\x\geq5\end{cases}\Rightarrow\begin{cases}x\in(-\infty;\;-10)\cup[6;\;+\infty)\\x\neq-10\\x\geq5\end{cases}\Rightarrow x\geq6$

$5.\\\begin{cases}x^2+2x-15>0\\x^2\geq36\end{cases}\Rightarrow\begin{cases}(x+5)(x-3)>0\\x\geq6\\x\leq-6\end{cases}\Rightarrow\begin{cases}x<-5\\x>3\\x\geq6\\x\leq-6\end{cases}\Rightarrow\\\\\\\Rightarrow x\in(-\infty;\;-6]\cup[6;\;+\infty)$