Предмет: Алгебра,
автор: n0name15
Розв'яжіть рівняння:
Приложения:
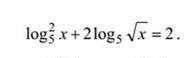
Ответы
Автор ответа:
0
Ответ:
х1=5 х2=1\25
Объяснение:
то квадратное уравнение, замена переменной Log5 (x)= Т
T^2+T-2=0
T1=1
T2=-2
Дальше обратная подстановка, с ОДЗ все согласуется (Х больше 0)
Автор ответа:
1
Ответ:
Объяснение:
ОДЗ: x>0.
Пусть log₅x=t ⇒
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Русский язык,
автор: Helen001
Предмет: Русский язык,
автор: maksimpergu
Предмет: Алгебра,
автор: 2000914