Предмет: Геометрия,
автор: ira33388
317.
Из начала координат, найти уравнения нарисованных касательных, для круга
(x - 4)² + (y - 2)² = 2.
класс какой
Ответы
Автор ответа:
1
........................................................
Приложения:
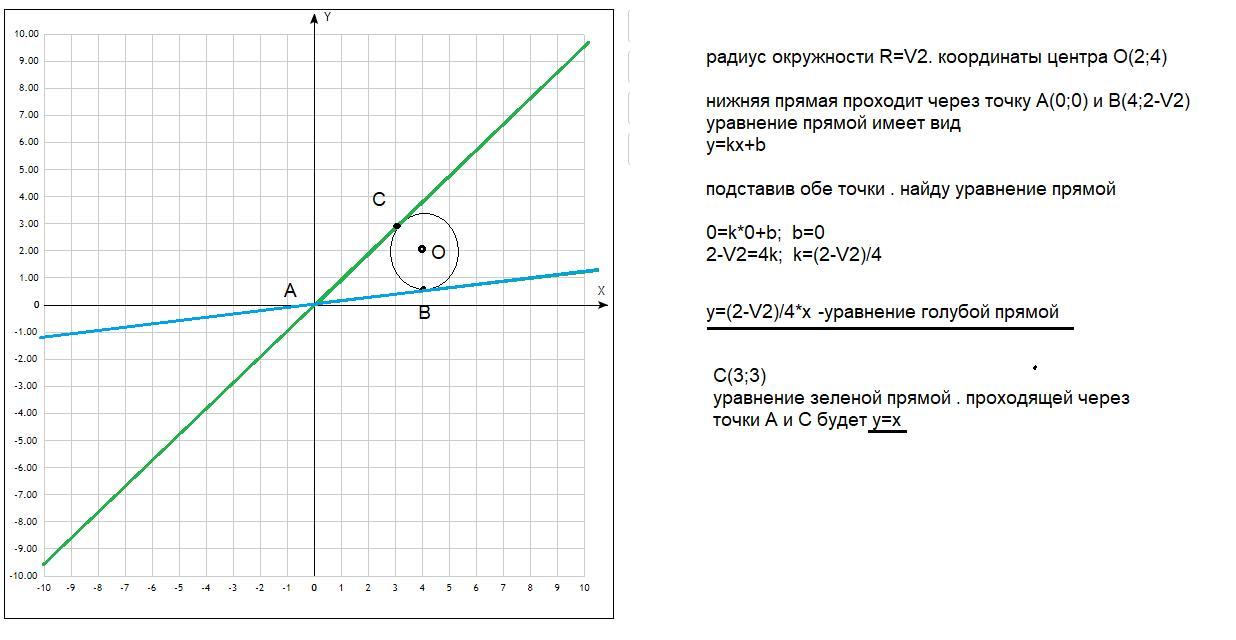
C зелёной (верхней касательной) всё сходится. А вот с нижней (синей) - нет. Точка B должна иметь координату x > 4.
т. В должна иметь координаты (4,2; 0,6)
ну вы ее координату тоже взяли ни откуда...
Да ладно.. И на этом спасибо!)
можно вывести точно, но не для 9 класса
Я в коледже учусь)
это даже хуже школы, там 10--11 за 1 год проходят
Координату взял по наклону 1/7 и -7. 7 клеточек на 1. Но реально задачи сложные. Возможно какая-то теория на эту тему хитрая есть.
Автор ответа:
1
Ответ:
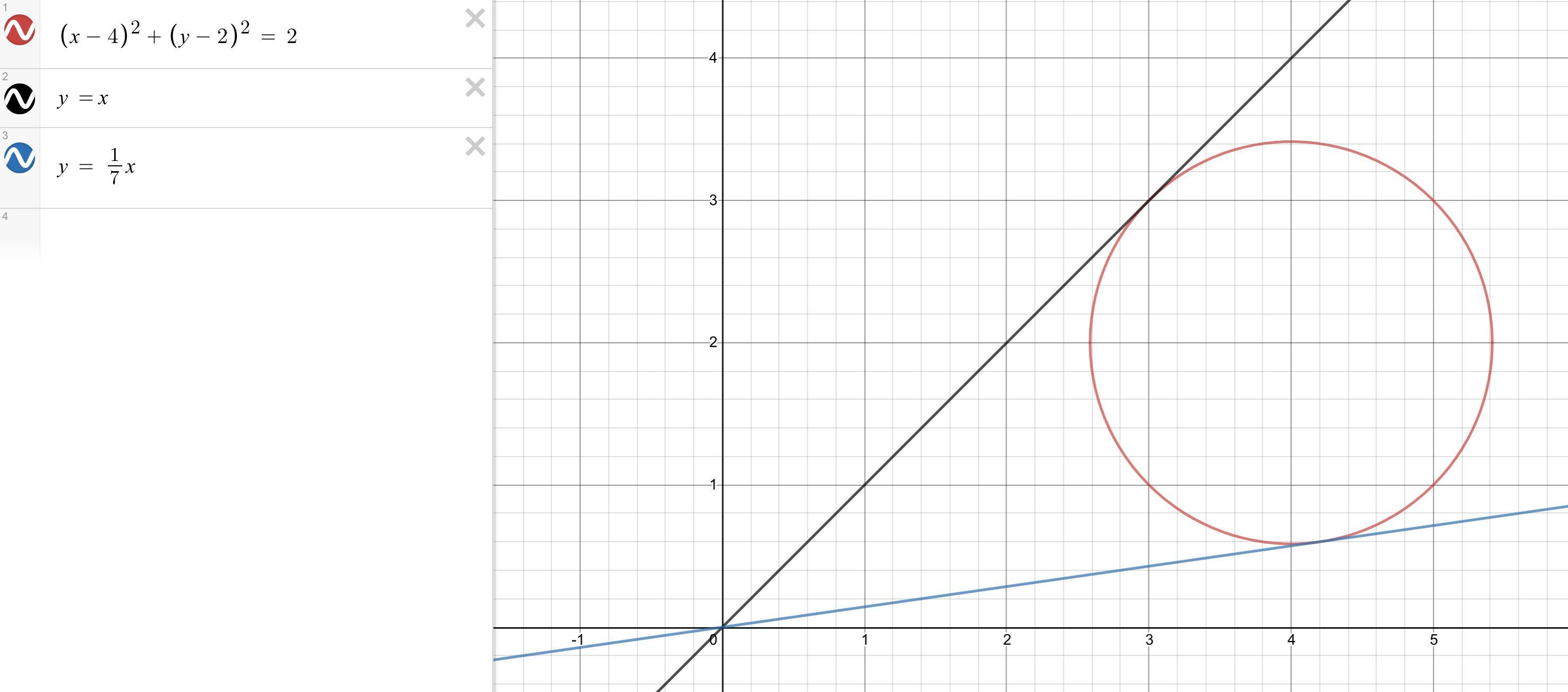
Уравнения касательных:
y = x
y = (1/7)*x
Объяснение:
Решение на рисунке.
Покажем, что т. A (3; 3) и т. B(4,2; 0,6) принадлежат как окружности, так и касаетльной.
(3 - 4)² + (3 - 2)² = 1 + 1 = 2, т.е. т. A на окружности.
Наклон графика (tan = 1) и наклон радиуса к tan = -1, т.е. радиус и касательная перпендикулятны.
(4,2 - 4)² + (0,6 - 2)² = 0,04 + 0,96 = 2
т. В лежит на окружности.
Наклон касательной tan = 1/7 и наклон радиуса tan = -7, т.е. радиус и касательная перпендикулярны.
Приложения:
ну вы и загнули!
Согласен. Мне моё решение не очень и самому нравится. По сути я угадал и доказал, что угадал правильно. По хорошему должен быть какой-то способ находить такие графики.
через производную
Через производную - это понятно. Но тут-то школа. Тут нужно без производных решать.
не школа оказалось
Похожие вопросы
Предмет: Другие предметы,
автор: Аноним
Предмет: Русский язык,
автор: egor002
Предмет: Другие предметы,
автор: Surk
Предмет: Математика,
автор: Катя122502
Похоже, что k1 = 1, а k2 = 1/7, т.е. касательные
y = x и y = x/7