Предмет: Геометрия,
автор: ivankoval19
помогите срочно!!!!.....................................
Приложения:

91anonimus91:
напечатай я решу сюда
вот похожая задача https://znanija.com/task/27439940
Ответы
Автор ответа:
1
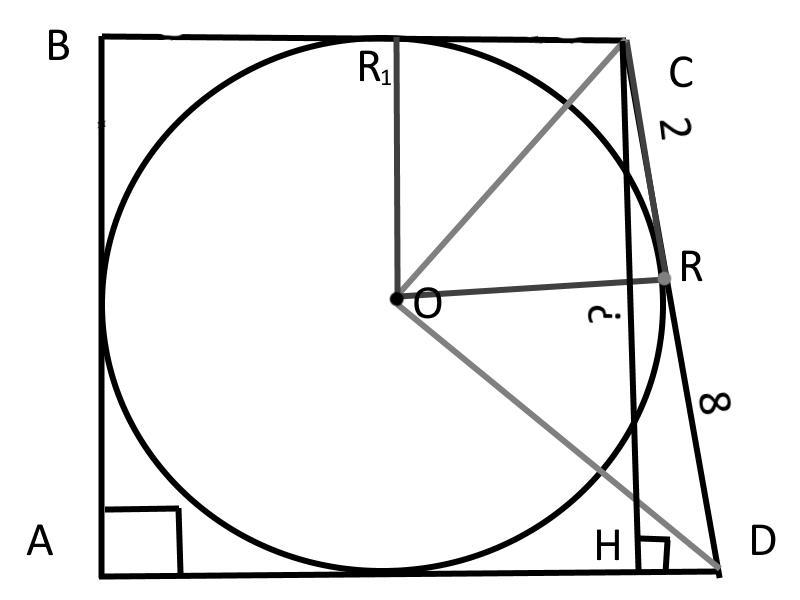
Если окружность можно вписать в трапецию, тогда сумма ее противоположных сторон - равна.
AB + CD = BC + AD;
CD = CR + RD = 2 + 8 = 10 см;
Пусть OR₁ - радиус, тогда
с теоремы о круге вписаном в трапецию:
OR₁ = (CH - Высота)
Со свойства круга вписаного в трапецию:
CR₁ = CR = 2 см;
Проведем радиус OR, перпендикулярный к CD, тогда:
∠COD = 90°, тогда по свойству метрических соотношений:
OR² = CR * RD ;
OR = ;
Из этого радиус равняется 4 см
Тогда с выше упомянутой теоремы (OR₁ = )
CH = 2OR₁ = 2OR = 2 * 4 = 8 см;
Ответ: 8 см.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Abogdanova82
Предмет: Русский язык,
автор: Царёшка
Предмет: Русский язык,
автор: svetavese
Предмет: Математика,
автор: Elvina66577
Предмет: История,
автор: batatany