Предмет: Геометрия,
автор: Miss778
Площадь основания конуса равна 9П, а площадь боковой поверхности равна 15П. Наидите радиус сферы вписанной в этот конус
Ответы
Автор ответа:
4
S ( основания)=π·R²
9π = π·R² ⇒ R²=9
R = 3 cм - радиус основания конуса
S( бок) = π·R·L
L- образующая конуса.
15π = π·3·L ⇒ L=5 cм
Осевое сечение конуса - равнобедренный треугольник, с боковыми сторонами L=5 cм и основанием , равным диаметру основания конуса, 6 см
Высота этого треугольника по теореме Пифагора
Н²=5²-3²=25-9=16
Н=4
Сфера, вписана в конус.
Значит ее большая окружность вписана в треугольник, являющийся осевым сечением конуса.
По формуле
Приложения:
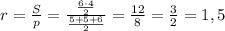
Похожие вопросы
Предмет: Українська мова,
автор: Mahka
Предмет: Английский язык,
автор: kukavageorge
Предмет: Русский язык,
автор: tatyanalapinaf
Предмет: Математика,
автор: анг32