Помогите решить пожалуйста
Ответы
Ответ:
Объяснение: ЗАДАНИЕ 2
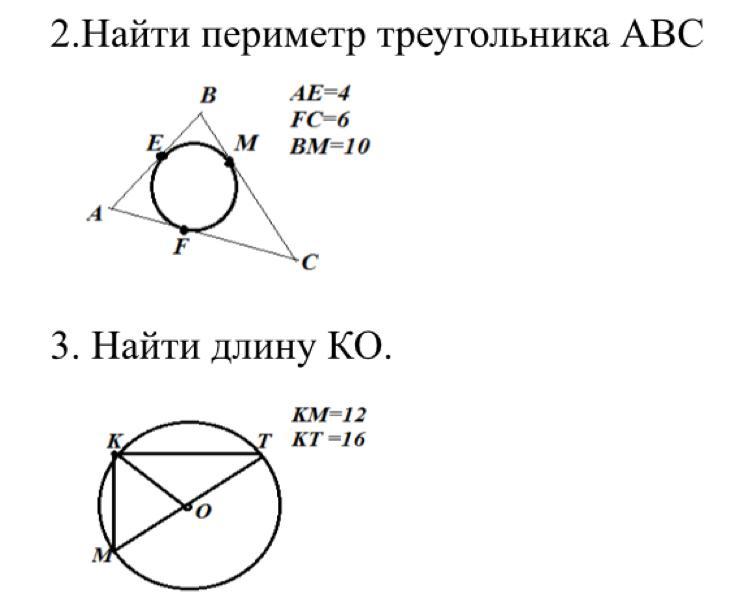
Стороны треугольника являются касательными к вписанной окружности поэтому отрезки касательных соединяясь в одной вершине равны от вершины до точки касания. Поэтому: АН=АР=4; ВМ=ВЕ=10; СМ=СF=6. Следовательно: АВ=4+10=14; ВС=10+6=16;
АС=4+6=10
Теперь найдём периметр треугольника зная его стороны:
Р=14+16+10=40
ОТВЕТ: Р=40
ЗАДАНИЕ 3
В нашем случае центр окружности находится в середине гипотенузы. Это свойство прямоугольного треугольника. Поэтому ∆МКТ- прямоугольный, в котором ТК и МК- катеты, а МТ- гипотенуза. Найдём гипотенузу по теореме Пифагора: МТ²=ТК²+МК²=
=16²+12²=256+144=400; МТ=√400=20
КО- является медианой ∆МКТ, поскольку делит его стороны пополам и ещё является радиусом ОК=ОТ=ОМ.
МТ является диаметром, поэтому радиусы ОК=ОТ=ОМ=20÷2=10
ОТВЕТ: ОК=10