Предмет: Алгебра,
автор: esdsi
ПРОШУ ПОМОГИТЕ ОЧЕНЬ НАДО! ДАМ 35 БАЛЛОВ
Приложения:
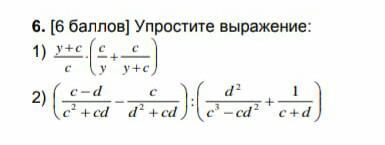
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Другие предметы,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Denchik2996
Предмет: Математика,
автор: vika1671
Предмет: Математика,
автор: Natali1791