Предмет: Алгебра,
автор: Магистр1Йода
Помогите решить неравенство,пожалуйста.
Приложения:
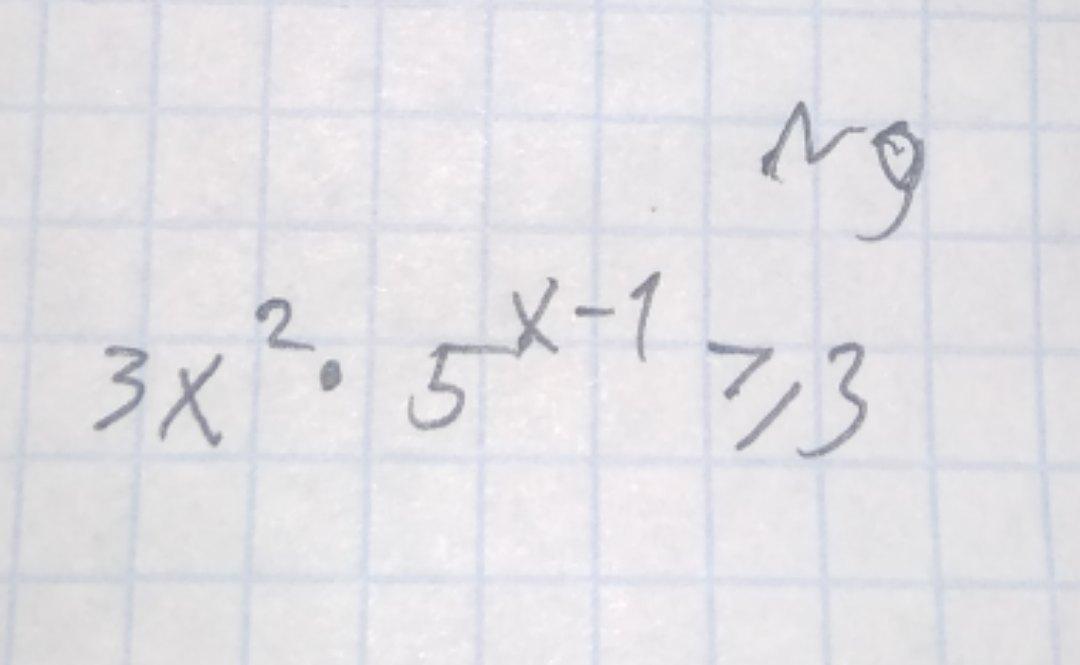
Ответы
Автор ответа:
1
Рассмотрим несколько промежутков.
Если то есть этот промежуток нам не подходит.
Если то есть этот промежуток нам подходит.
Пусть Этот промежуток самый сложный, поскольку на нем функция
убывает, а функция
возрастает. Применим математический анализ для исследования.
Приравниваем производную к нулю для нахождения точек экстремума.
На нашем промежутке находится точка
Слева от этой точки производная положительна (не забывайте про x в начале, который на нашем промежутке отрицательный), справа отрицательна. Следовательно, это точка максимума. Найдем значение функции в этой точке:
Поскольку
на этом участке функция меньше 1, то есть этот участок нам не подходит.
Ответ:
Похожие вопросы
Предмет: Українська мова,
автор: lera2003fox
Предмет: Русский язык,
автор: Angel12007
Предмет: Українська мова,
автор: vovaroy
Предмет: Литература,
автор: fkztujhjdf
Предмет: Математика,
автор: вахаааа