Помогите пожалуйста: 50 + 25 баллов
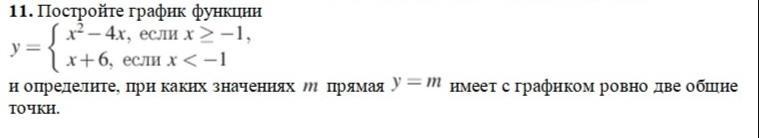
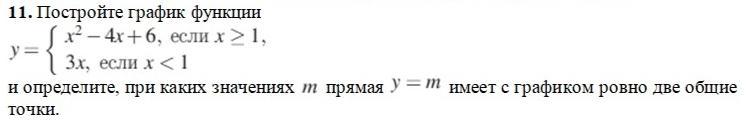
Ответы
Ответ:
Объяснение:
Идея построения в следующем: строим полный график и выделяем нужный кусочек
1) Строим график функции у=х^2-4х на всей числовой прямой, а затем выделяем ту часть графика, которая лежит правее прямой х=-1
график функции у=х^2-4х- парабола с ветвями вверх. Точки пересечения с осями координат
ох, у=0, поэтому х^2-4х=0
х(х-4)=0
х=0 или х=4
оу, х=0, тогда у=0-4*0=0
вершина параболы- это точка с координатами( -в/2а; у)
х=4:(2*1)=2, у(2)=2^2-4*2=-4
Строим параболу.
2) Строим график функции у=х+6 на всей числовой прямой, а затем выделяем ту часть графика, которая лежит левее прямой х=-1
график функции у=х+6- прямая, для построения берем две любые точки плюс одна контрольная
х=о, у=6
х=4, у=10
х=-1, у=5 Строим прямую
3)Соединяем два кусочка в один график, получим кусочную функцию
В Рaint получилось не очень аккуратно, но начертишь аналогично в тетради и будет великолепно
Ответ:
Задание 1. 2 общие точки — при m = -4 и m = 5;
Задание 2. 2 общие точки — при m = 2 и m = 3.
Объяснение:
Такая запись уравнения означает, что если х больше или равен -1, уравнение функции имеет вид y = , а если х меньше -1, то у функции другое уравнение — y = x+6.
Чтобы построить график такой функции, нужно построить в одной координатной плоскости графики обоих уравнений (из первой и второй строки).
1. , причём х ≥ -1. Графиком такой функции является парабола, ветви которой направлены вверх. Координаты её вершины можно рассчитать по формуле
х(верш) = , где а — коэффициент при
(то есть 1), b — коэффициент при х (то есть -4). Тогда
х(верш) =
Теперь найдём координату вершины по оси у. Для этого подставим координату х вершины в уравнение функции
y(верш) =
Значит, вершина параболы имеет координаты (2; -4).
Пользуясь уравнением , найдём координаты других точек, принадлежащих графику (при этом не следует забывать, что, по условию, х не может быть меньше -1):
х = 1
y =
х = 0
у =
х = -1 (неравенство нестрогое (знак «больше или равно»), значит, эта точка принадлежит этому графику).
у =
х = 3
у =
х = 4
у =
х = 5
у =
Начертим координатную плоскость, отметим в ней точки (2; -4), (1; -3),
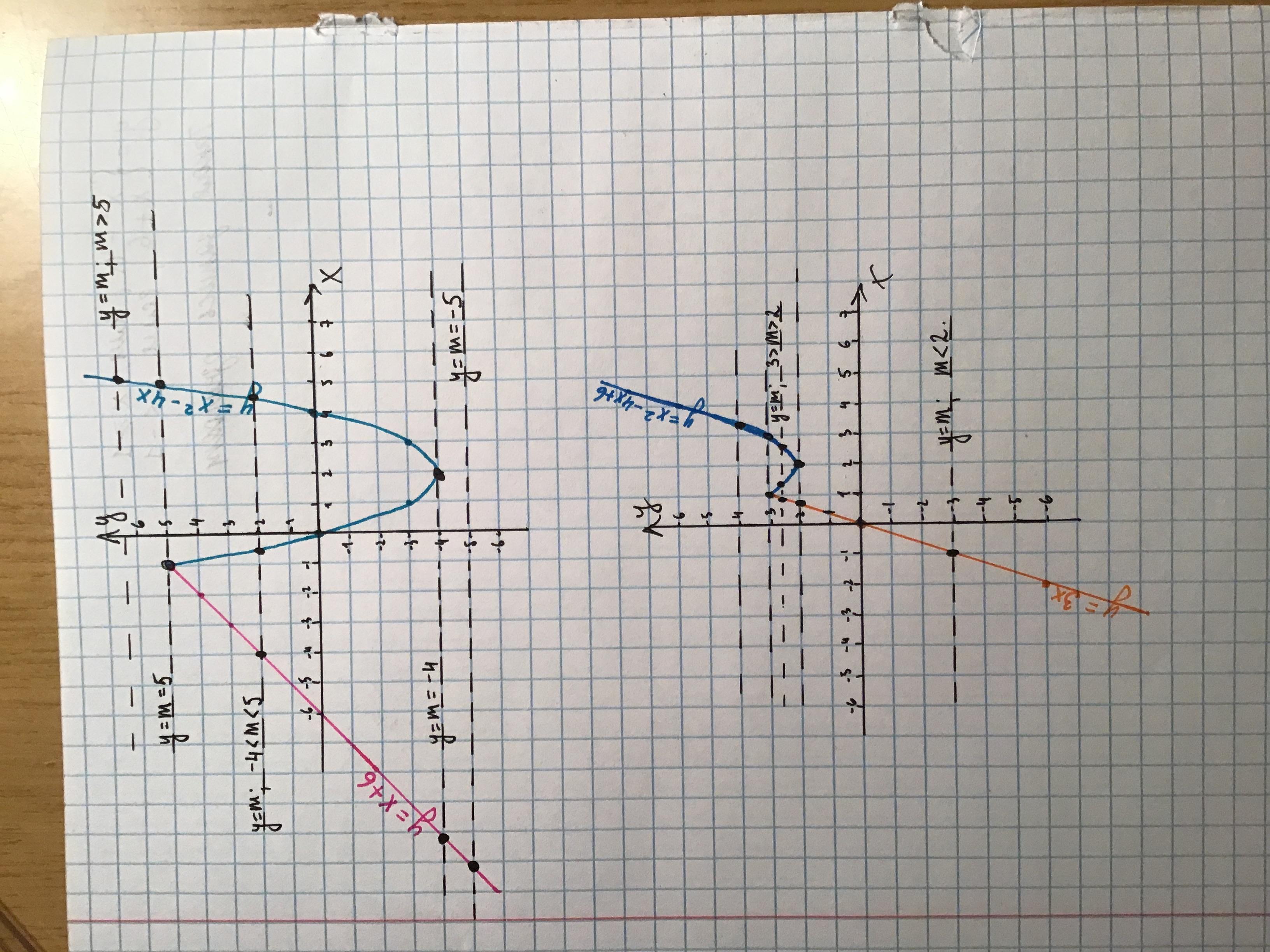
(0; 0), (-1; 5), (3; -3), (4; 0) и (5; 5). Соединив их, получим график функции, заданной первой строкой (см. бирюзовый график на рисунке).
Перейдём ко второй строке. В ней сказано, что
у = х + 6, если х < -1. Графиком такой функции является прямая. Учитывая, что х не может быть больше или равным -1, найдём координаты точек, принадлежащих графику, подставляя различные х в уравнение у = х + 6:
х = -2
у = -2 + 6 = 4
х = -3
у = -3 + 6 = 3
Для построения прямой этих двух точек достаточно. Отметим их на координатной плоскости и, соединив их, построим график (см. розовый график на рисунке).
График y = m представляет собой горизонтальную прямую, параллельную оси х.
Обратимся к построенному графику функции. На графике видно, что если горизонтальная линия пройдёт ниже вершины параболы (то есть если y=m будет меньше -4), эта линия будет иметь с графиком только одну общую точку (для наглядности точки пересечения выделены на рисунке чёрным). Значит, любые значения m меньше -4 нам не подходят.
Если прямая y = m пройдёт через вершину параболы (в этом случае y = m = -4), она будет иметь с графиком две общие точки.
При значениях m больше -4 и до 5 прямая y = m пересекае график в трёх точках. Этот промежуток не подходит.
При m = 5 прямая y = m пересекает график в двух точках.
При m > 5 прямая y = m имеет с графиком только одну общую точку. Этот промежуток тоже не подходит.
Итак, прямая y = m пересекает график функции ровно в двух точках только при m = -4 и m = 5.
Задание 2.
Подобная запись означает, что если х больше или равен 1, график функции задаётся уравнением ,
а если х меньше 1, функция задаётся уравнением y = 3x.
Как и в предыдущем задании, чтобы построить график этой функции, нужно построить в одной координатной плоскости графики обеих строк.
1. При х ≥ 1 график строится по уравнению . График этой функции — парабола, ветви которой направлены вверх. Координаты параболы найдём по формуле
х(верш) =
Чтобы найти у(верш), подставим 2 вместо х в уравнение функции:
у(верш) =
Вершина расположена в точке с координатами (2; 2).
Теперь вычислим координаты других точек, принадлежащих графику (учитывая, что х не меньше 1):
х = 1
у =
х = 3
у =
х = 4
у =
Отметив эти точки, построим график (см. голубой график на рисунке).
Перейдём ко второй строчке. В ней сказано, что если х меньше 1, у = 3х.
Графиком такой функции является прямая. Найдём координаты её точек, учитывая, что х < 1:
х = 0
у = 3*0 = 0
х = -1
у = 3*(-1) = -3
х = -2
у = 3*(-2) = -6
Отметив эти точки на коорд. плоскости, получим график (см. оранжевый график на рисунке).
Найдём значения m, при которых прямая y = m (как уже известно, это горизонтальная прямая) имеет с графиком две общие точки.
На графике видно, что если m меньше 2, прямая y = m имеет с графиком только одну общую точку.
Если m = 2, прямая y = m проходит через вершину параболы и имеет с графиком две общие точки.
Затем, если m больше 2, но меньше 3, прямая y = m имеет с графиком 3 общие точки, а при m = 3 — две общие точки.
При m > 3 прямая y = m имеет с графиком только одну общую точку.
Значит, прямая y = m имеет с графиком функции ровно две общие точки при m = 2 и m = 3.