Question

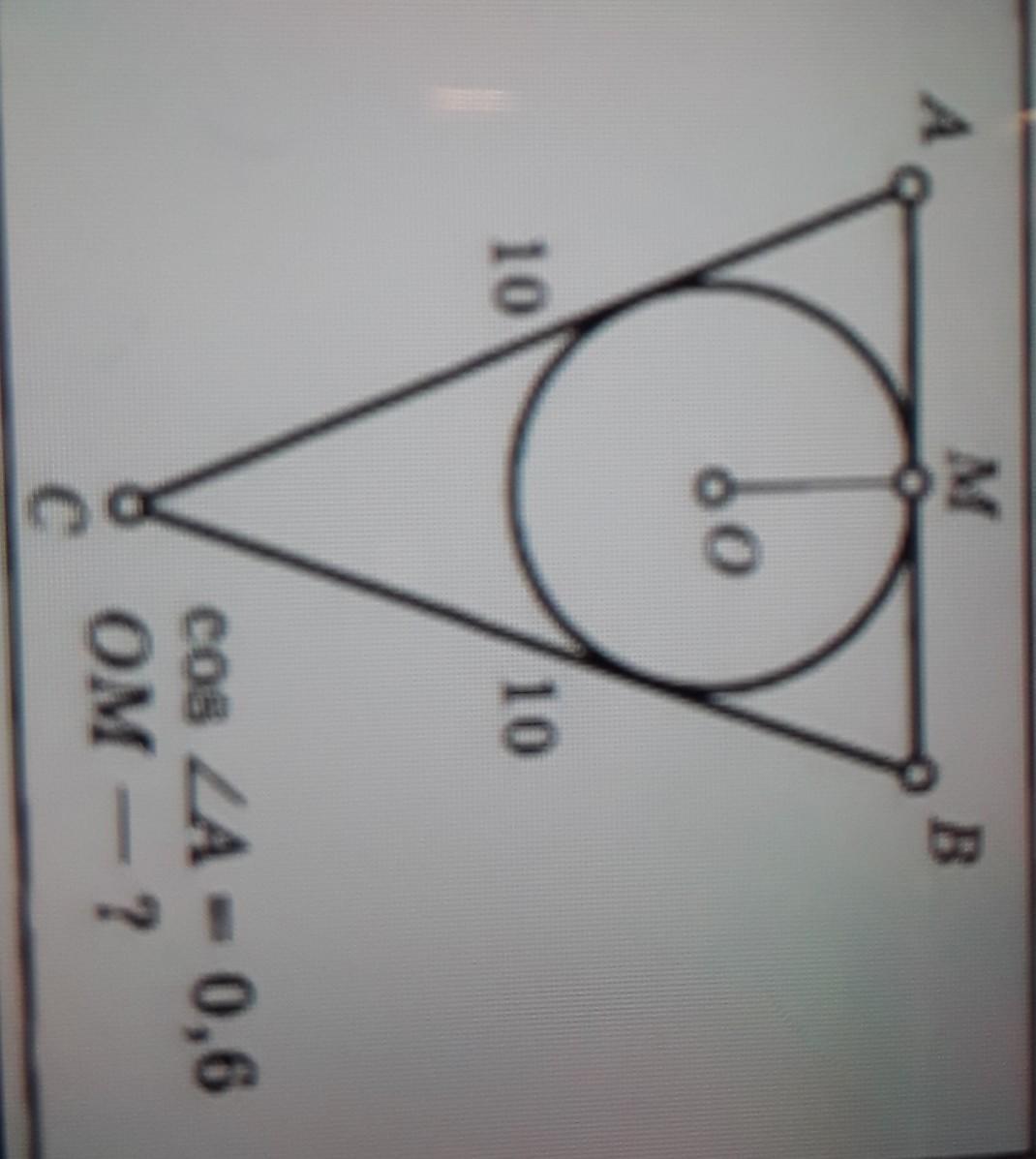
Треугольник АВС вписан в лкружность. АС=ВС=10. соs А=0,6. Найти ОМ​. Пожалуйста, помогите СЕГОДНЯ, прошу

Answer 1

Найти: OM

1. проведём прямую от точки М до точки С. эта прямая будет делить равнобедренный треугольник ABC на два рввных прямоугольных треугольника - ACM и BCM.

2. рассмотрим прямоугольный треугольник АСМ:

cos угла А = отношению катета АМ к гипотенузе АС

cos угла А=0,6 по условию и

АС=10 по условию,

тогда получаем отношение

6/10=АМ/10

отсуда следует, что АМ=6=МВ т.к. прямоугольные треугольники АСМ и ВСМ равны

ВА=АМ+МВ=12 - основание треугольника АВС

3. OM=радиусу окружности вписанной в равнобедренный треугольник АВС

радиус вписанной окружности в произвольном треугольнике можно найти по формуле:

$r = \sqrt{ \frac{(p - a)(p - b)(p - c)}{p} }$

где p - полупериметр, равный ½•(a+b+c)

в нашем случае:

½•(AC+CB+BA), где АС=СВ=10, ВА= 12

p=½•(10+10+12)=½•32=16

радиус вписанной окружности равен:

$r = \sqrt{ \frac{(16 - 10)(16 - 10)(16 - 12)}{16} } \\ r = \sqrt{ \frac{6 \times6 \times 4 }{16} } \\ r = \sqrt{ \frac{144}{16} } \\ r = \frac{12}{4} \\ r = 3$

OM=3 см

ответ: 3 см