Предмет: Алгебра,
автор: idel655
Найти неопределенный интеграл и результаты интегрирования проверить дифференцированием
Приложения:
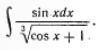
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Английский язык,
автор: onlygod
Предмет: Русский язык,
автор: rbaktiiar
Предмет: Русский язык,
автор: adfdf55
Предмет: Математика,
автор: егор1177
Предмет: Математика,
автор: Аноним