Решите систему неравенств
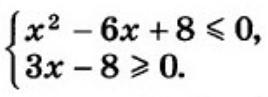
Ответы
Ответ:
[8/3, 4], решение системы неравенств.
Объяснение:
Решить систему неравенств:
х²-6х+8<=0
3x-8>=0
Решим первое неравенство как квадратное уравнение:
х²-6х+8=0
х₁,₂=(6±√36-32)/2
х₁,₂=(6±√4)/2
х₁,₂=(6±2)/2
х₁=4/2=2
х₂=8/2=4
Смотрим на уравнение. Уравнение параболы.
Начертим СХЕМУ параболы (ничего вычислять не нужно), которую выражает уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= 2 и х=4. По графику ясно видно, что у<=0 (как в неравенстве) между значений х, то есть, решения неравенства в интервале х∈ [2, 4].
Значения х= 2 и х=4 входят в число решений неравенства, скобка квадратная.
Решим второе неравенство.
3x-8>=0
3x>=8
x>=8/3
х∈[8/3, +∞), решение второго неравенства.
Неравенство нестрогое, скобка квадратная.
Теперь на числовой оси нужно отметить оба интервала и найти пересечение решений, которое подходит двум неравенствам.
Отмечаем на числовой оси числа 2; 8/3 (≈2,7); 4.
Штриховка от 2 до 4, от 4 до 2; от 8/3 (2,7) до + бесконечности.
Пересечение [8/3, 4], это и есть решение системы неравенств.