Предмет: Геометрия,
автор: madiar6
Дано прямоугольный треугольник АВС, с угла А проведена биссектриса АК на сторону ВС, с точки К проведен перпендикуляр АК отрезок КN на сторону АВ, при этом АВ=3NB. Доказать ВК=АК
Приложения:
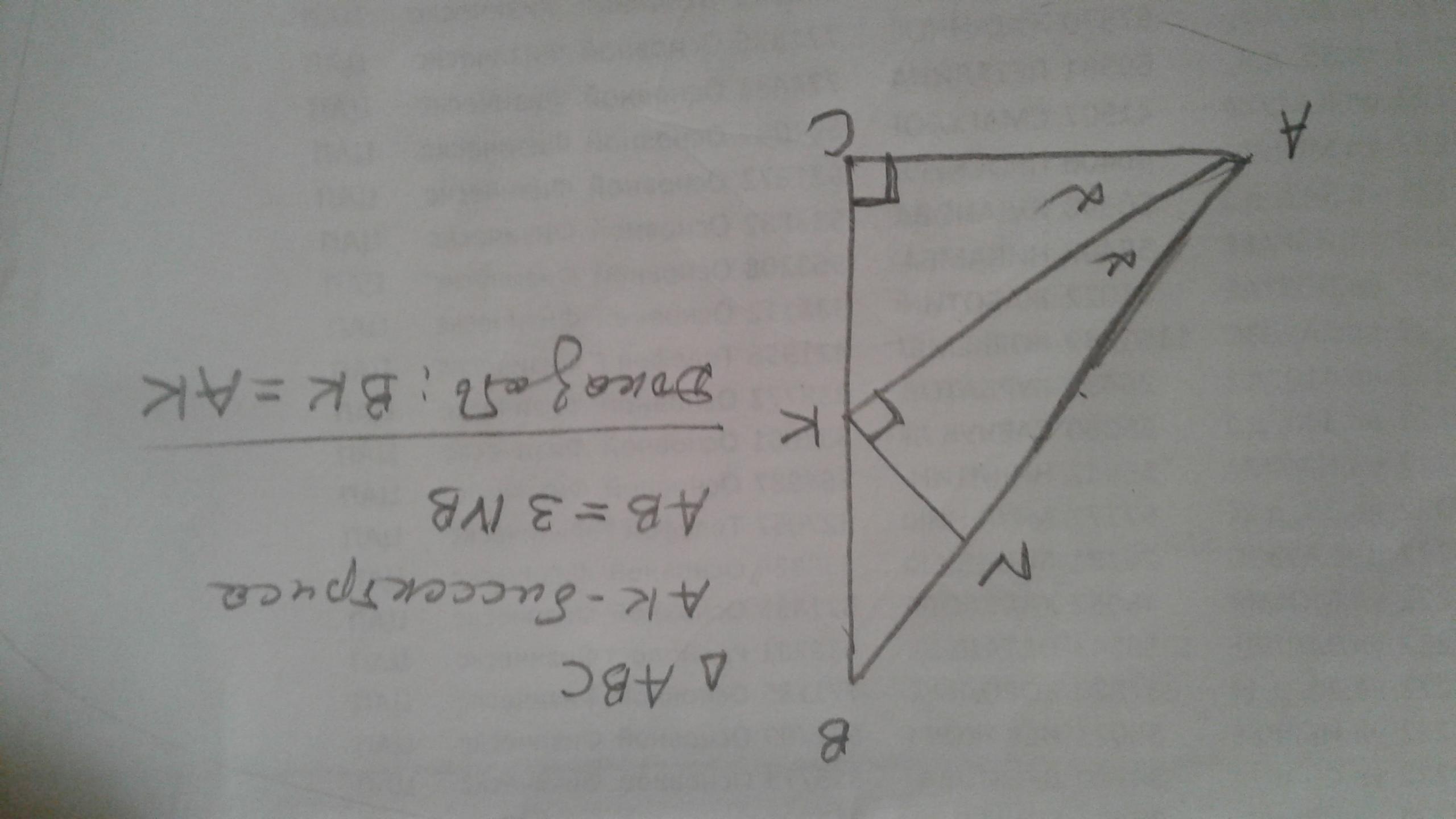
ded911:
Проверьте данные. А то не получается доказать.
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Не уверен, но вариант такой:
Т.к. АВ=3NB, то AN=2NB, следовательно AN в два раза больше NB, а значит углы напроив этих сторон отличаются в два раза и следовательно угол BKN в два раза меньше угла NKA (который 90 град), получаем, что угол NKB равен 45 град.
Тогда угол AKC 180-90-45 = 45 град.
Тогда угол KAC 180-90-45 = 45 град. Значит треугольник АКС прямоугольный равнобедренный и АС=СК и так как АК биссектриса, то СК=ВК и = АС.
Для прямоугольного треугольника АКС получаем
квадрат АК= квадрату АС + квадрат КС
квадрат АК = квадрат ВК + квадрат ВК
АК = ВК х
Похожие вопросы
Предмет: Русский язык,
автор: портная
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: Салтанат1111111