Question

Пожалуйста срочно!!! Даю 35 баллов с подробным решением и рисунком пожалуйста!!!

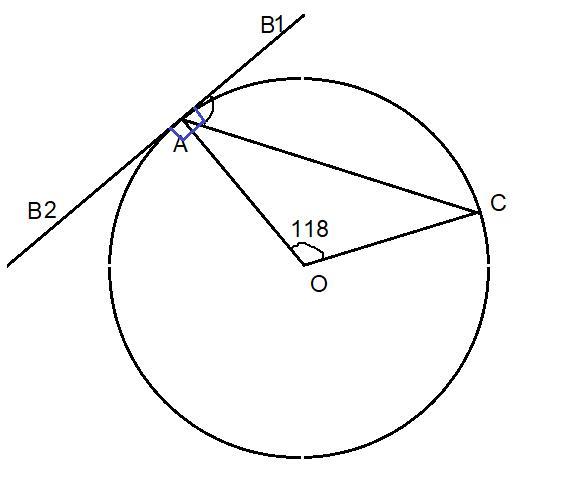
У колі з центром у точці О проведено хорду АС та дотичну АВ, точка А – точка дотику кола та прямої. Знайдіть величину <САВ, якщо <АОС = 118⁰ .

Answer 1

Ответ:

∠САВ1 = 59°

∠САВ2  = 121°

Пошаговое объяснение:

см. рис

ΔAOC - равнобедренный АО=ОС

∠ОАС = ∠ОСА = (180 - 118)/2 = 62/2 = 31°

∠OAB1 = ∠OAB2 = 90° (свойство касательной)

∠САВ1 = ∠ОАВ1 - ∠ОАС = 90 - 31 = 59°

∠САВ2 = ∠ОАВ2 + ∠ОАС = 90 + 31 = 121°

Answer 2

Ответ:

59°

Пошаговое объяснение:

Розглянемо ΔАОС - рівнобедрений, бо утворений радіусами кола.

∠ОАС=∠ОСА=(180-118):2=31°

∠ОАВ=90°, бо утворений радіусом та дотичною

∠САВ=∠ОАВ-∠ОАС=90-31=59°