Question

Пожалуйста решите задачу по геометрии! Очень прошу вас.
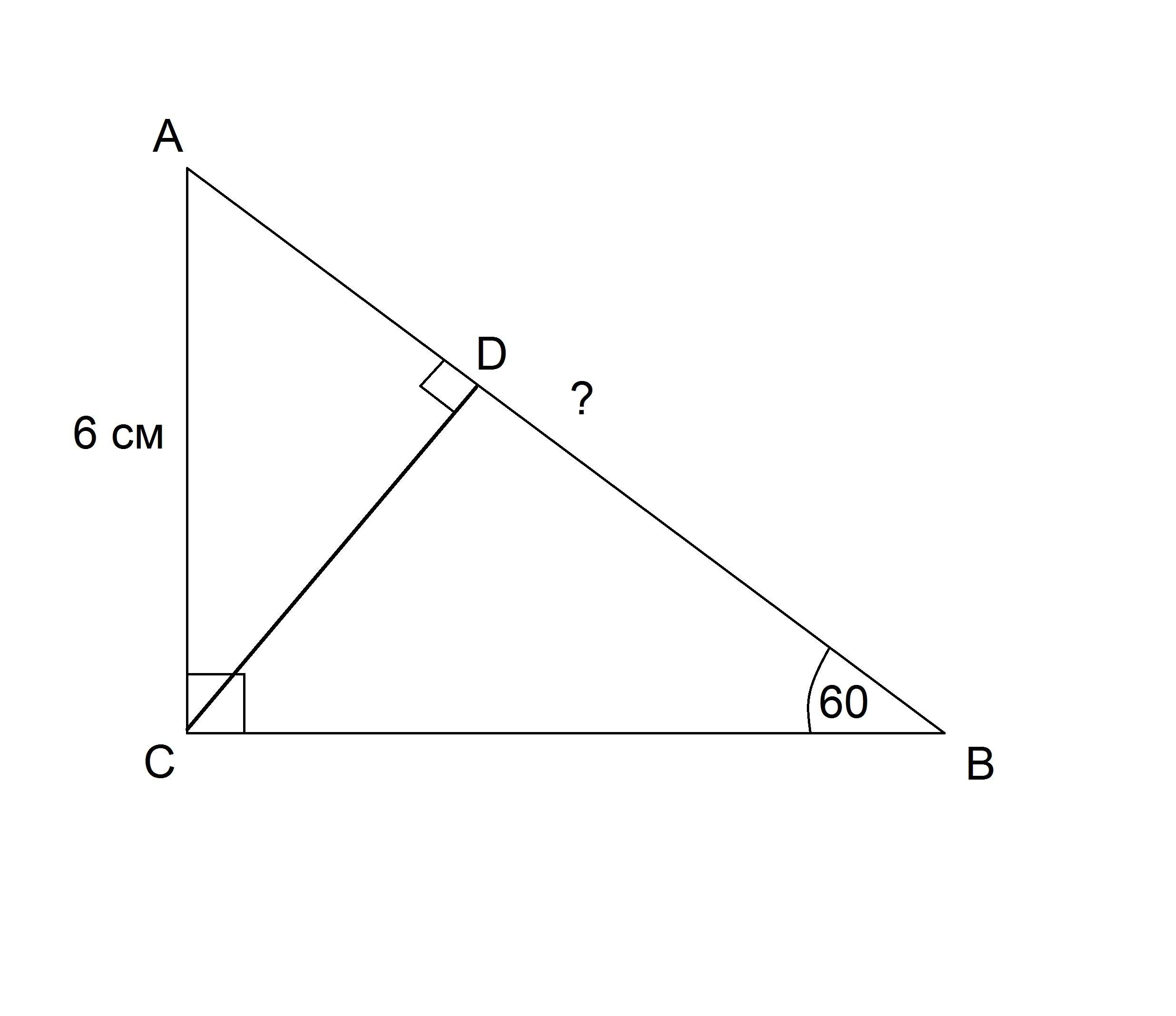
В прямоугольном треугольнике ABC угол С = 90 градусов, АС = 6 см, Угол АВС = 60 градусам. Найдите: а) АB; б) высоту СD, проведенную к гипотенузе.

Answer 1

Дано: ΔABC - прямоугольный, ∠C = 90°, ∠ABC = 60°, AC = 6 см.

Найти: а) AB; б) CD

Решение: 1) Рассмотрим ΔABC: ∠ABC = 60°, ∠C = 90°, ∠A = 30° (т. к. 180° - (90° + 60°) = 30); Найдем сторону AB через синус угла ABC (синус острого угла равен отношению противолежащего катета к гипотенузе): sin60° = $\frac{\sqrt{3}}{2}$ = $\frac{AC}{AB\\}$ = $\frac{6}{AB}$; Отсюда AB = $\frac{2*6}{\sqrt{3} }$ = $\frac{12}{\sqrt{3} }$ см.

2) Рассмотрим ΔACD, в котором ∠D = 90°, а ∠CAD = 30° (из 1); Согласно свойству прямоугольного треугольника с углом в 30°, катет, лежащий напротив угла в 30°, равен половине гипотенузы, следовательно, CD = 1/2*AC = 1/2*6 = 3 см.

Ответ: а) $\frac{12}{\sqrt{3} }$ см; б) CD = 3 см.