Предмет: Геометрия,
автор: hfriju
Вычисли полупериметр ромба, радиус и площадь круга,
если ∢ MLK =60° и OM = 12 мм, а площадь ромба равна 283–√3мм2.
Приложения:
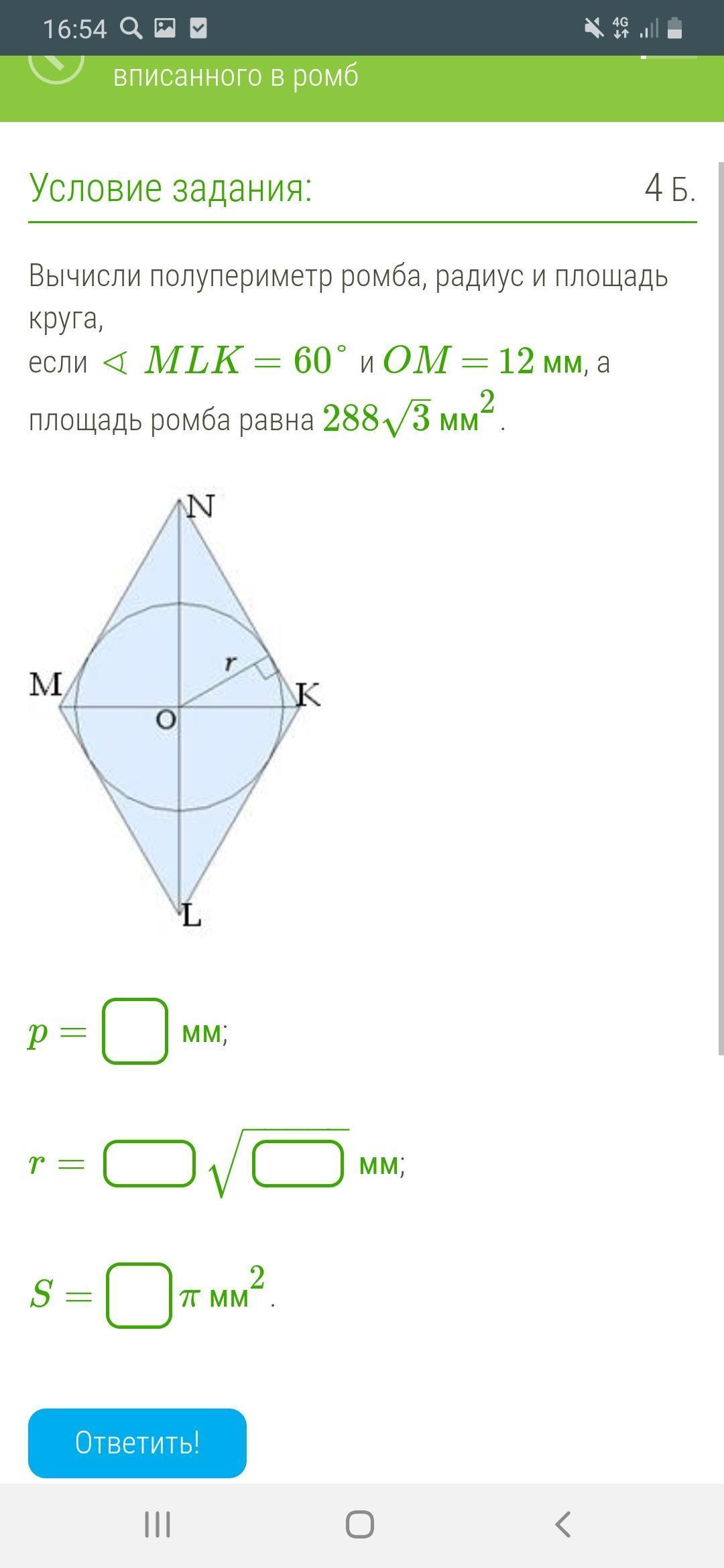
Ответы
Автор ответа:
19
∢К=∢М=180-60=120°
MK=12*2=24
--------------------------
S ромба=0,5*d1*d2
Обозначим вторую диагональ(NL) через х:
288√3=0,5*24*x
Х=24√3(NL)
По теореме Пифагора найдём сторону ромба:
(12√3)²+12²=432+144=576
√576=24
Мы знаем что все стороны ромба одинаковые, найдём периметр:
Р=24+24+24+24=96мм
р=96÷2=48мм
------------------------------------------------
∢ МКN=120÷2=60
Значит другой угол равен:
180-(60+90)=30°(∢О)
По теореме сторона лежащий против 30° равен половине гипотенузы:
Гипотенуза ОК=12
12÷2=6(катет)
По теореме Пифагора найдём другой катет(r)
144-36=108
r=√108=6√3
Площадь круга:
S=пr²=108п
Ответ:
р=48мм
r=6√3 мм
S=108п
Похожие вопросы
Предмет: Русский язык,
автор: ramir03
Предмет: Русский язык,
автор: заремка222
Предмет: Английский язык,
автор: 2003146
Предмет: Литература,
автор: LiZoChKa1234LiZoChKa
Предмет: Литература,
автор: KotICzaDrotIK