Предмет: Геометрия,
автор: laraket58
Trijst_vien_paz12.png
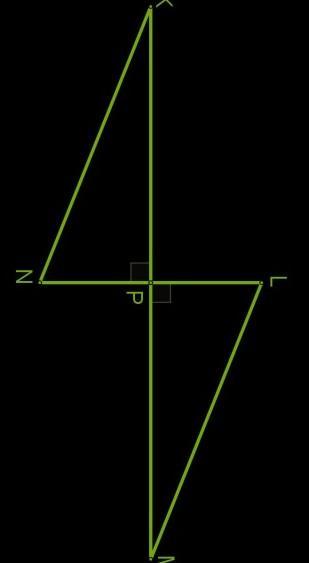
Два перпендикулярных отрезка KM и LN пересекаются в общей серединной точке P.
Какой величины∡ N и ∡ K, если ∡ L = 40° и ∡ M = 50°?
1. Отрезки делятся пополам, значит, KP =
,
= LP,
∡
= ∡ MPL, так как прямые перпендикулярны и оба угла равны
°.
По первому признаку равенства треугольник KPN равен треугольнику MPL.
2. В равных треугольниках соответствующие углы равны.
В этих треугольниках соответствующие ∡
и ∡ M, ∡
и∡ L.
∡ K =
°;
∡ N =
°.
Приложения:
densungkim:
Можно картинку с эти заданием. А то запутался. Вроде в начале описание название картинки, но это не ссылка.
прикрепила
Ответы
Автор ответа:
3
Ответ:
L=N=40
M=K=50
KP = PM
KPN=MPL
Объяснение:
Отрезки пересекаясь создают 2 абсолютно одинаковых треугольника. Из-за этого у них все части друг другу равны. Просто обозначены другими буквами.
Похожие вопросы
Предмет: Английский язык,
автор: kolchk
Предмет: Русский язык,
автор: nastya164
Предмет: Русский язык,
автор: heghine
Предмет: Информатика,
автор: zloisolovey
Предмет: Математика,
автор: valeralipin