Предмет: Геометрия,
автор: xiops764
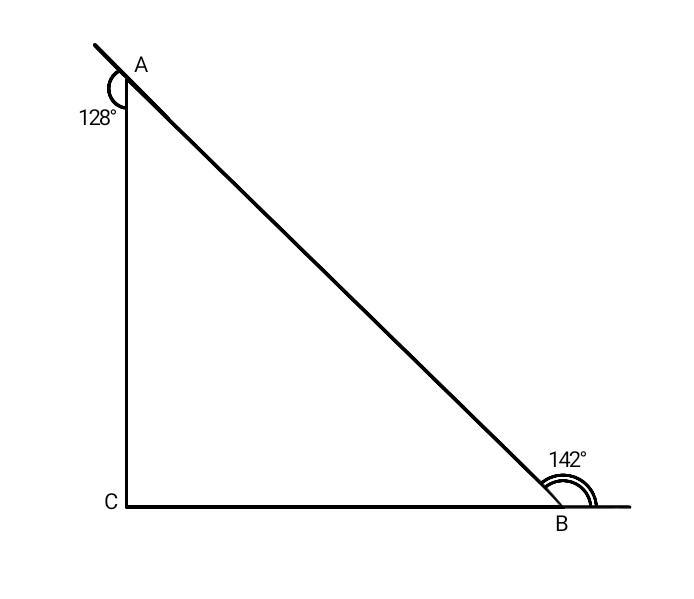
докажите что треугольник АВС является прямоугольными если внешние углы треугольника при вершинах А и В 128 и 142 градуса
Ответы
Автор ответа:
2
Дано:
∆АВС.
Внешний угол А = 128°.
Внешний угол В = 142°.
Доказать:
∆АВС - прямоугольный.
Доказательство:
Угол САВ = 180°-128° = 52° (так как они смежные).
Угол АВС = 180°-142° = 38° (так как они тоже смежные).
Угол САВ+ угол АВС = 52°+38° = 90°.
А если сумма двух углов треугольника равна 90° , то такой треугольник - прямоугольный. => ∆АВС - прямоугольный.
Ответ: что требовалось доказать.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: Veyrons
Предмет: Українська література,
автор: zoryanamanko
Предмет: Математика,
автор: nastasyastasen
Предмет: Математика,
автор: SusannaMuratov