Предмет: Геометрия,
автор: Kabachokdjodjo
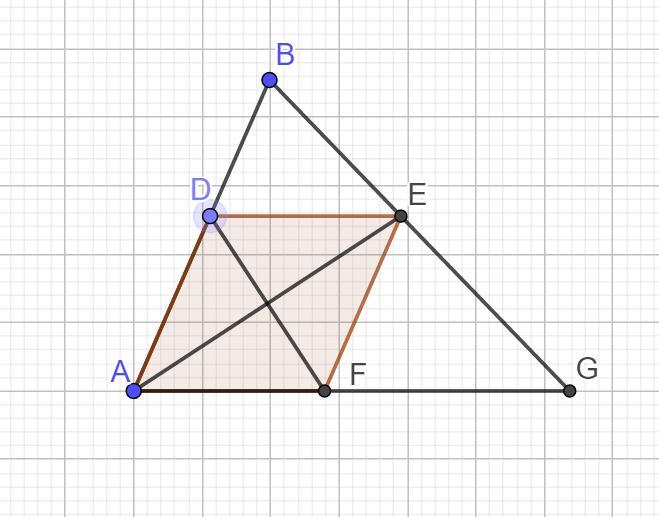
В треугольник вписан ромб так, что один угол у них общий, а противоположная вершина делит сторону треугольника в отношении 2:3. Диагонали ромба равны m и n. Найти стороны треугольника, содержащие стороны ромба.
dnepr1:
Как это понять: "Диагонали ромба равны тип."?
Ответы
Автор ответа:
3
Пусть сторона ромба равна а.
По свойству ромба а = √((m/2)² + (n/2)²).
Треугольники ВДЕ и АВС подобны к = 2/(2 + 3) = 2/5.
Тогда находим сторону АС = (5/2)*а = (5/2)*√((m/2)² + (n/2)²).
Диагональ ромба АЕ - биссектриса угла А.
По свойству биссектрисы:
АВ = (2/3)АС = (2/3)*(5/2)√((m/2)² + (n/2)²) = (5/3)√((m/2)² + (n/2)²).
Ответ: АВ = (5/3)√((m/2)² + (n/2)²),
АС = (5/2)√((m/2)² + (n/2)²).
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Русский язык,
автор: Mizuda
Предмет: Русский язык,
автор: milasha44
Предмет: Математика,
автор: mardanova34
Предмет: Геометрия,
автор: ScarletGhost451