Question

Очень нужно. Пожалуйста

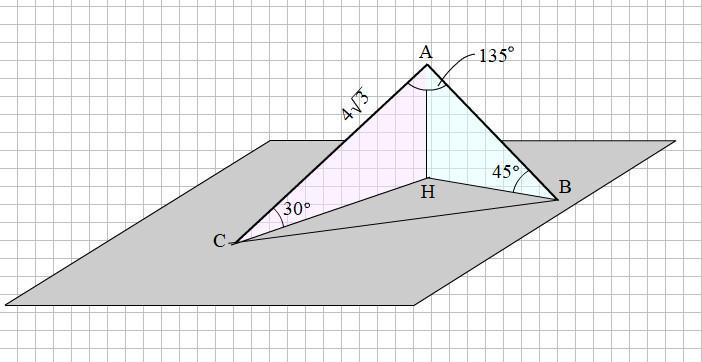
Из точки А к плоскости альфа проведены наклонные АВ и АС, образующие с плоскостью углы 45° и 30° соответственно, а угол между наклонными равен 135°. Найдите расстояние между точками В и С, если АС = 4√3 см.

Answer 1

Ответ:

BC = 2√30 см ≈ 11 см

Объяснение:

Смотри прикреплённый рисунок.

Расстояние от точки А до плоскости

АН = АС · sin 30² = 4√3 · 0.5 = 2√3 (см)

Наклонная АВ равна

АВ = АН : sin 45° = 2√3 : 0.5√2 = 2√6 (см)

По теореме косинусов найдём расстояние ВС

ВС² = АВ² + АС² - 2 · АВ · АС · cos 135° =

= 24 + 48 - 2 · 2√6  · 4√3 · (-0.5 √2) =

= 72 + 48 = 120

BC = √120 = 2√30 (см)