Предмет: Геометрия,
автор: ABC1234567
Найдите боковое ребро треугольной пирамиды.высота которой проходит через центр окружности .описанной около основания.если стороны основания пирамиды равны 50 .78, 112.а высота равна 72
Ответы
Автор ответа:
0
Формула радиуса описанной окружности треугольника:
R=abc:4S
Площадь треугольника по формуле Герона равна корню из произведения полупериметра (p) на разности полупериметра треугольника и каждой из его сторон (a, b, c):
S=√{p(p−a)(p−b)(p−c)}
Не буду приводить вычисления, их несложно сделать самостоятельно.
По формуле Герона найдем площадь треугольника - она равна 1680 см²
Радиус, найденный по приведенной выше формуле радиуса описанной окружности,
равен 65 см.
Расстояние от центра описанной окружности до каждой из вершин треугольника одинаково,
является проекцией каждого ребра и равно радиусу этой окружности.
Высота пирамиды и проекция ребер - катеты прямоугольных треугольников и одинаковы для каждого ребра, которые в этих треугольниках являются гипотенузой.
По т. Пифагора длину ребра найти несложно.
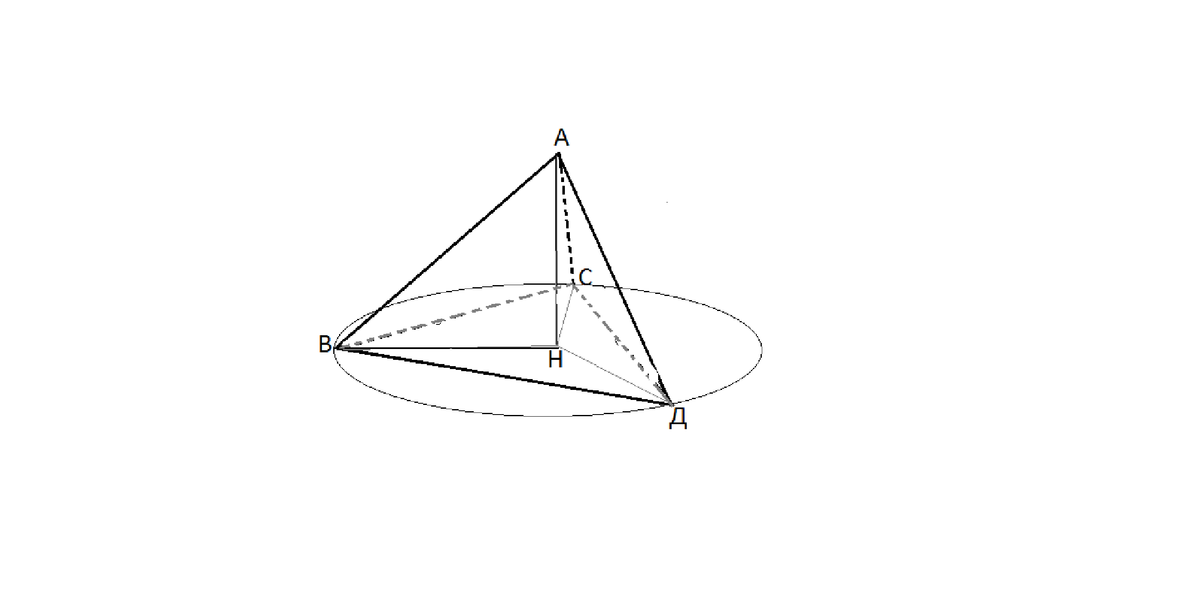
В данном случае АВ=АД=АС =√(АН²+ВН²)=√(72²+65²)=97 см
R=abc:4S
Площадь треугольника по формуле Герона равна корню из произведения полупериметра (p) на разности полупериметра треугольника и каждой из его сторон (a, b, c):
S=√{p(p−a)(p−b)(p−c)}
Не буду приводить вычисления, их несложно сделать самостоятельно.
По формуле Герона найдем площадь треугольника - она равна 1680 см²
Радиус, найденный по приведенной выше формуле радиуса описанной окружности,
равен 65 см.
Расстояние от центра описанной окружности до каждой из вершин треугольника одинаково,
является проекцией каждого ребра и равно радиусу этой окружности.
Высота пирамиды и проекция ребер - катеты прямоугольных треугольников и одинаковы для каждого ребра, которые в этих треугольниках являются гипотенузой.
По т. Пифагора длину ребра найти несложно.
В данном случае АВ=АД=АС =√(АН²+ВН²)=√(72²+65²)=97 см
Приложения:
Похожие вопросы
Предмет: Физика,
автор: gassizgood
Предмет: Химия,
автор: yrabassw
Предмет: Английский язык,
автор: inzuzoldyhanova37
Предмет: Литература,
автор: Аноним