Предмет: Алгебра,
автор: stalker1992ru
Логарифмическое неравенство.
Приложения:
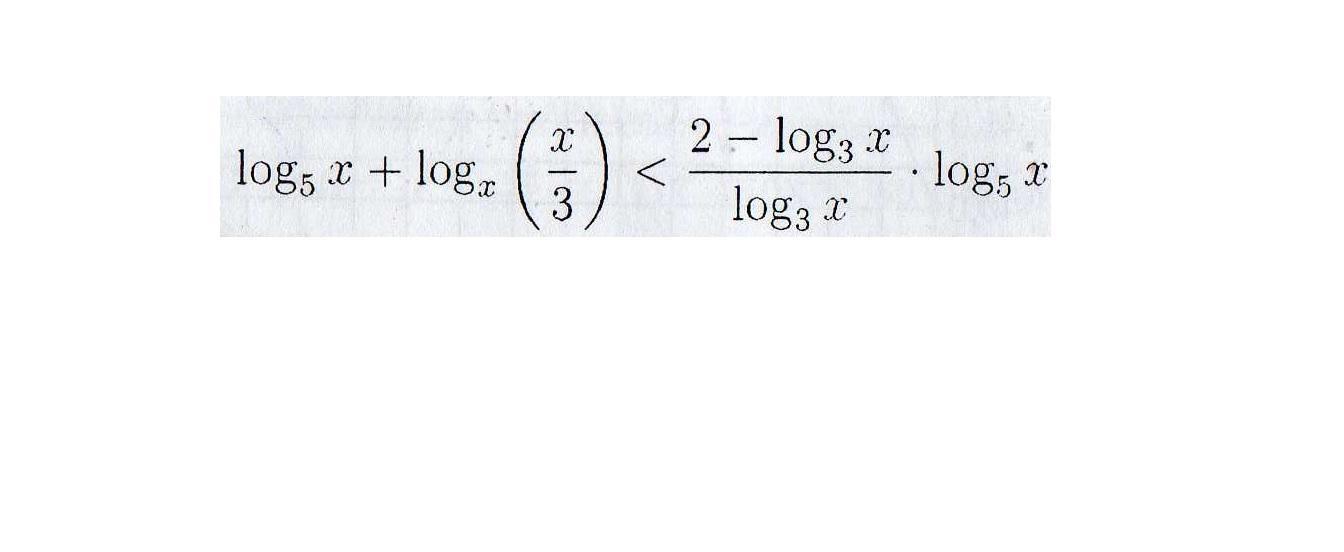
Ответы
Автор ответа:
1
Ответ:
Объяснение:
ОДЗ: x > 0, x ≠ 1
С учётом ОДЗ
Похожие вопросы
Предмет: Русский язык,
автор: Джесся
Предмет: Английский язык,
автор: джов666
Предмет: Английский язык,
автор: polinagromova0
Предмет: Математика,
автор: zhiza26
Предмет: Математика,
автор: darinabessolova