Предмет: Геометрия,
автор: оникова
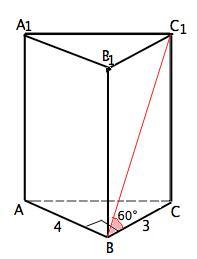
найдите площадь боковой поверхности треугольной призмы ABCA1B1C1 если в основании призмы лежит прямоугольный треугольник ABC с катетами AB=4 и BC=3, а угол C1BC РАВЕН 60 градусов
Ответы
Автор ответа:
1
Ответ: 36√3 (ед. площади)
Объяснение:
Площадь боковой поверхности прямой призмы равна произведению высоты на периметр основания.
Поскольку в условии нет дополнительных указаний, призма прямая и все её боковые грани - прямоугольники.
Ѕ( бок)=Р•Н
Р(АВС)=АВ+ВС+АС.
Катеты основания 3 и 4 ⇒ треугольник «египетски» с гипотенузой 5 (можно вычислить и по т.Пифагора). АС=5, Р(АВС)=5+3+4=12
Высота Н призмы СС1=ВС•tg60°=3√3
S(бок)=(3√3)•12=36√3 (ед. площади)
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: torolai
Предмет: Русский язык,
автор: ДимаБондарев
Предмет: Другие предметы,
автор: ocen159
Предмет: Математика,
автор: умник1348