СРОЧНО ПЖПЖПЖПЖПЖ ПОМОГИТЕ (с решением)
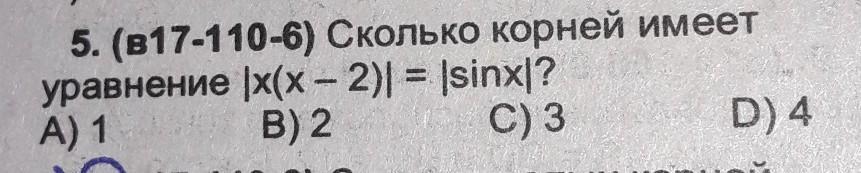
Ответы
Интересная задача. Правда, вряд ли она по силам школьникам в 9 классе. По крайней мере моё решение использует производную, которую в школе (насколько я знаю) изучают не раньше 10-го класса.
Первый пункт решения показывает, как избавиться от модуля в уравнении вида |a|=|b|. Используя геометрическое определение модуля как расстояние до начала координат, получаем, что такое уравнение равносильно совокупности
В нашем случае получаем совокупность
Тем самым задача сводится к нахождению нулей функций
и
1) Мы видим, что вторая производная всюду больше нуля, что говорит о том, что функция вогнута на всей прямой (иными словами, первая производная постоянно растет). Далее,
f(0)=0 (один корень уже найден), причем f'(0)<0. Поскольку производная растет, делаем вывод, что слева от нуля она будет отрицательной, поэтому функция там убывает, а раз в нуле функция равна нулю, слева от нуля функция положительна, то есть там корней быть не может.
Справа же от нуля (раз f'(0)<0) функция сначала станет отрицательной, но в силу возрастания производной скорость ее убывания замедляется, а в какой-то момент функция достигнет своего минимума и начнет монотонно расти, причем в какой-то момент станет положительной (например, f(3)>0) и продолжит расти. Поэтому где-то графику функции придется пересечь ось OX, но только один раз (не считая x=0). Таким образом, суммарно f(x) в двух точках обращается в ноль.
2) Снова вторая производная положительна, то есть эта функция вогнута. Снова g(0)=0, g'(0)<0. В результате g(x) (как и f(x)) справа от нуля еще в одной точке обратится в ноль.
3) Итак, f(x) обращается в ноль в двух точках, и g(x) обращается в ноль в двух точках. Всего четыре? Конечно, нет, ведь одна из точек общая - это 0. Значит, всего три? Да, это так, только мы должны ещё проверить, что вторые точки, где функции обращаются в ноль, не совпадают. Это легко. Поскольку в такой точке функции должны совпадать, получаем
Если n=0, получаем x=0 - но эту точку мы уже отметили в решении. Если же n не равно нулю, то есть
Ответ: 3