Question

Помогите пж НУЖНО СРОЧНО!!!!!!

Answer 1

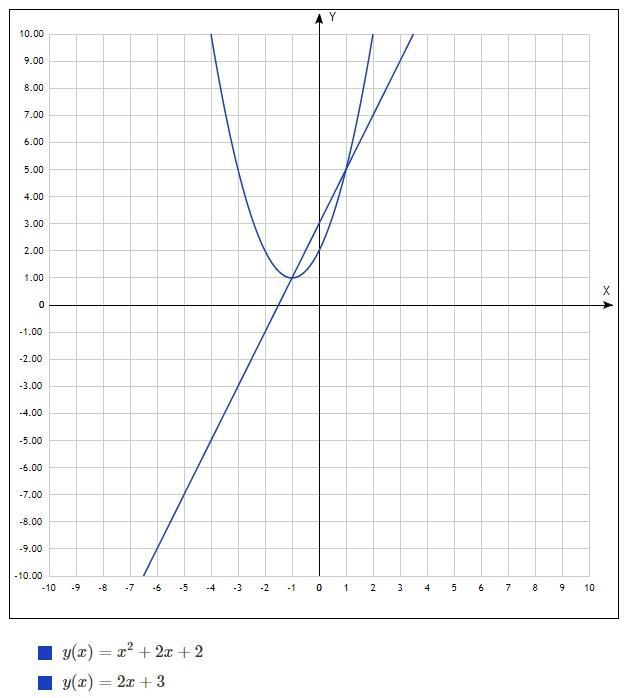
Для начала нужно построить параболу и прямую.

Параболу можно привести в чуть более удобный виде:

$y=x^2+2x+2=x^2+2x+1+1=(x+1)^2+1$ - то это обычная шаблонная парабола, но смещенная на 1 ед. влево по ОХ и на 1 ед. вверх по ОУ.

Прямую по двум точкам строим. Когда построили, увидели, что нужно найти площадь того кусочка, где прямая выше параболы. Чтобы найти эту площадь, нужно вспомнить соответствующую теорему. Суть её в том, что если на некотором промежутке $f(x)\geq g(x)$ (в нашем случае прямая и парабола), то площадь такого участка находится как интеграл от разности двух функций (кстати, даже неважно даже, как по отношении к оси ОХ располагаются обе функции), то есть

$S = \int\limits^b_a {(f(x)-g(x))} \, dx$

В нашем случае корни (для интегрирования - пределы) легко находятся графически, но так бывает не всегда, поэтому найдем их аналитически, решим уравнение:

$x^2+2x+2=2x+3 \Rightarrow x^2-1=0 \Rightarrow x^2=1 \Rightarrow x=\pm1$

Когда пределы известны, можно и интегрировать:

$\displaystyle S = \int\limits^1_{-1} {(2x+3-(x^2+2x+2))} \, dx =\int\limits^1_{-1} {(-x^2+1)} \, dx =\bigg(-\frac{x^3}{3}+x\bigg)\bigg|\limits^1_{-1} =\\=-\frac{1^3}{3}+1-\bigg(-\frac{(-1)^3}{3} +(-1)\bigg) =\frac{2}{3}-\bigg(\frac{1}{3}-1\bigg) = \frac{2}{3}-\bigg(-\frac{2}{3} \bigg )=\frac{4}{3}$

Ответ: площадь получившейся фигуры равна $1\dfrac{1}{3}$