Question

Выберите правильный ответ.
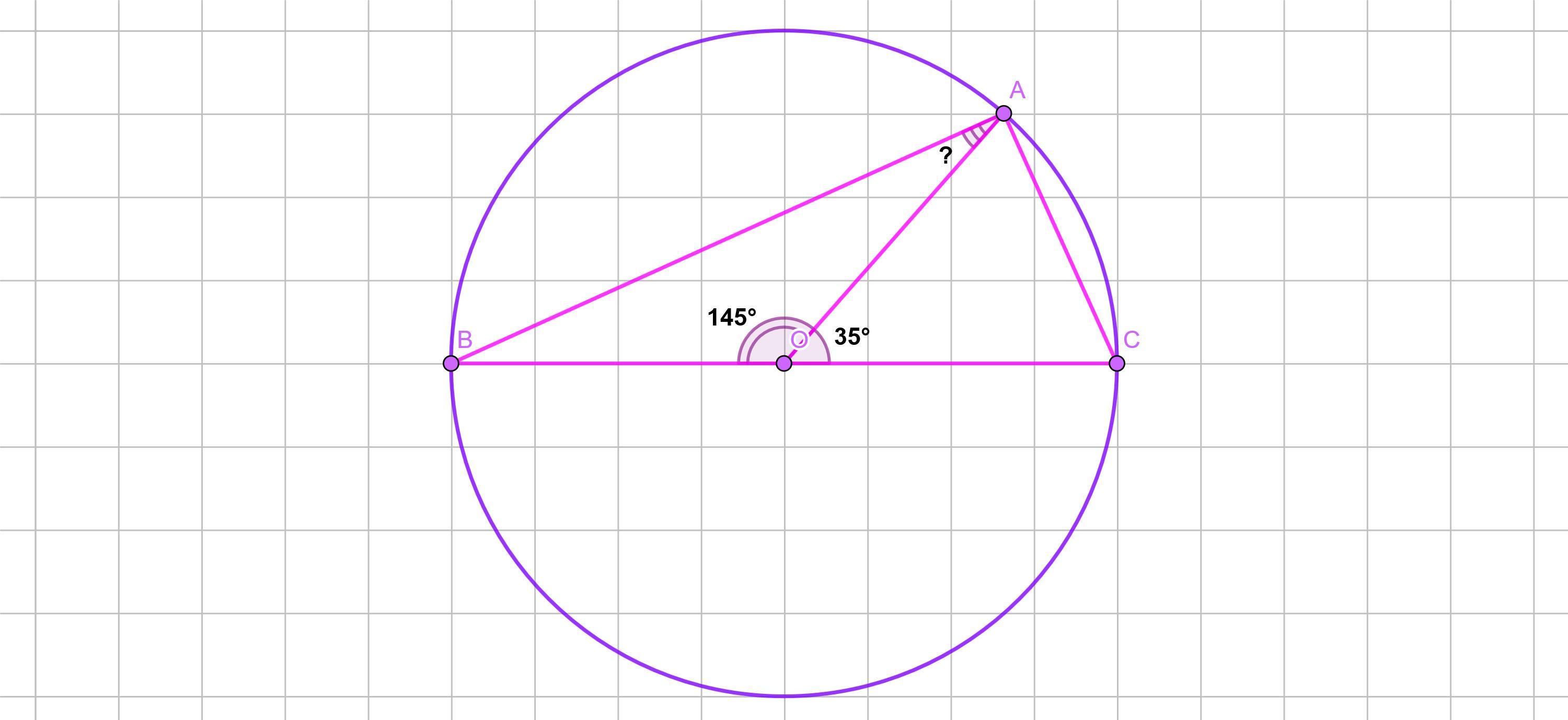
Отрезок BC – диаметр окружности с центром O. На окружности взяли точку A так, что ∠AOC = 35°. Найдите градусную меру угла BAO.
Можно с решение пожалуйста очень срочно

Answer 1

Дано:

Окружность с центром О.

ВС - диаметр.

А ∈ окружности с центром О.

∠АОС = 35°

Найти:

∠ВАО - ?

Решение:

1 способ.

Так как АО и ОВ - радиусы данной окружности с центром О ⇒ △ВОА - равнобедренный.

∠ОВА = ∠ВАО, по свойству равнобедренного треугольника.

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

⇒ ∠ВАО + ∠ОВА = 35° (∠АОС = 35°, по условию)

Так как ∠ОВА = ∠ВАО, по свойству ⇒ ∠ОВА = ∠ВАО = 35°/2 = 17,5°

2 способ.

Так как АО и ОВ - радиусы данной окружности с центром О ⇒ △ВОА - равнобедренный.

∠ОВА = ∠ВАО, по свойству равнобедренного треугольника.

Сумма смежных углов равна 180°.

∠АОС смежный с ∠ВОА ⇒ ∠ВОА = 180° - 35° = 145°

Сумма углов треугольника равна 180°.

⇒ ∠ВАО =  ∠ОВА = (180° - 145°)/2 = 17,5°

Ответ: 17,5°.