Предмет: Алгебра,
автор: vipandrey109
Помогите решить уравнения.
Приложения:
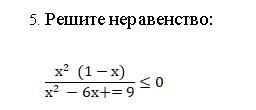
superstrong:
в знаменателе ошибка
Как учительница написала )) Так и буду делать ))) Красава
Ответы
Автор ответа:
1
Ответ:
х=0 и х ≥ 1, за исключением х = 3, то есть х 3
Объяснение:
x² всегда больше или равен 0. При х=0 выражение также равно 0 и неравенство справедливо.
Знаменатель - 6х + 9 = (х-3)² также всегда больше или равен 0. Необходимо учесть, что при х = 3 деление на ноль невозможно.
Следовательно, неравенство сводится к виду 1 - х ≤ 0
Значит х=0 и х ≥ 1, за исключением х = 3.
Автор ответа:
1
х²(1-х)/(х²-6х+9)≤0
х²(1-х)/(х-3)²≤0 х-3≠0; х≠3
х²≥0; (х-3)²>0
чтобы дробь была ≤0, надо чтобы (1-х)≤0
х≥1
Ответ: х≠3; х=0; х≥1
-----------------[0]------------[1]-------------(3)------------------->x
\\ \\\\\\\\\\\\\\\\ \\\\\\\\\\\\\\\\\\\\\\\
x∈[0]U[1; 3)U(3; ∞) - это ответ.
это вам спасибо
а можете помоч еще 1 пример? просто соч делаю )
(х^2 +x +6 >0/x^2 <25 это один пример
сможете ?
Похожие вопросы
Предмет: Другие предметы,
автор: said20031
Предмет: Русский язык,
автор: reality227
Предмет: Английский язык,
автор: Юлькина
Предмет: Биология,
автор: irinadoroxova
Предмет: Обществознание,
автор: 129034785