Предмет: Алгебра,
автор: kikirikialex74
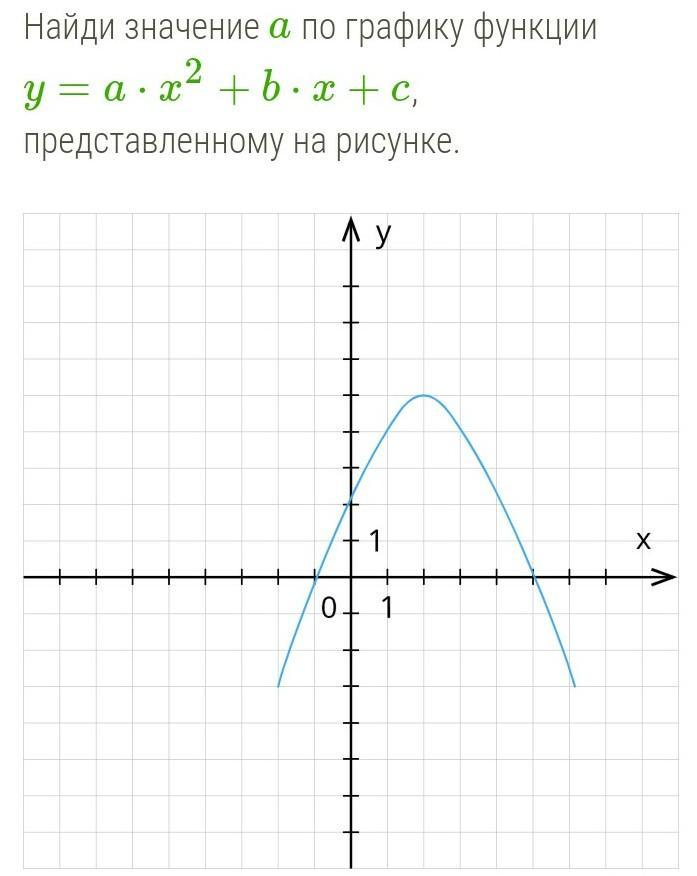
Помогите с алгеброй
Приложения:
Ответы
Автор ответа:
1
Відповідь:
Пояснення:
Если для уравнения известны координаты 3-х различных точек его графика
, то его коэффициент а можно будет знайтии так:
kikirikialex74:
Спасибо
Не за что
Можно лучший ответ))
Похожие вопросы
Предмет: Русский язык,
автор: Мариночка0111
Предмет: Українська мова,
автор: kosturiaoleg
Предмет: Английский язык,
автор: ЛОЛОШОК
Предмет: Математика,
автор: dtimashewa