Question

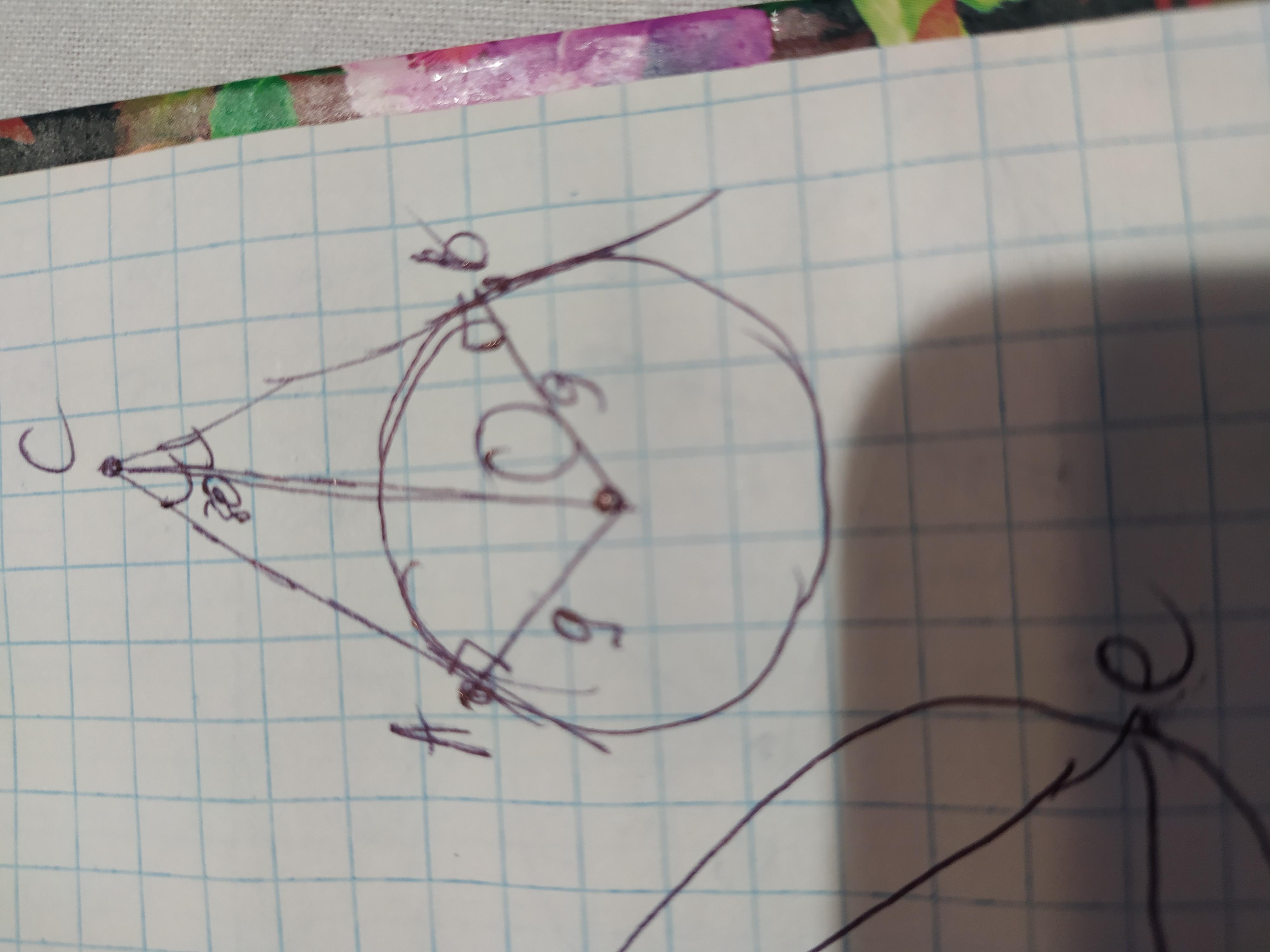
3. СВ и СА – отрезки касательных, проведенные к окружности радиуса 9 см, с центром в точке О. Найдите СВ и СА, если ∟ОСА =30°.

Answer 1

Ответ: 9√3см

Объяснение: проведём к касательным радиус, они образуют прямой угол 90°. Также рассмотрим ∆АСО и ВСО. Они прямоугольные и равны, поскольку А и В соединяются в одной точке С, поэтому АС=ВС; АО=ВО=радиусу=9см, ОС- общая сторона. Из этого следует что угол ОСА=углу ОСВ=30°. Угол лежащий напротив угла 30° равен половине гипотенузы, поэтому АО=½СО. СО=9×2=18см; СО=18см. Теперь найдём по теореме Пифагора АС. АС=√(СО²-АО²) =√(18²-9²)=√(324-81)=

=√243=√81×√3=9√3;

Итак: АС=ВС=9√3см