Предмет: Геометрия,
автор: loopomogite849645
HELP ME, PLEASE
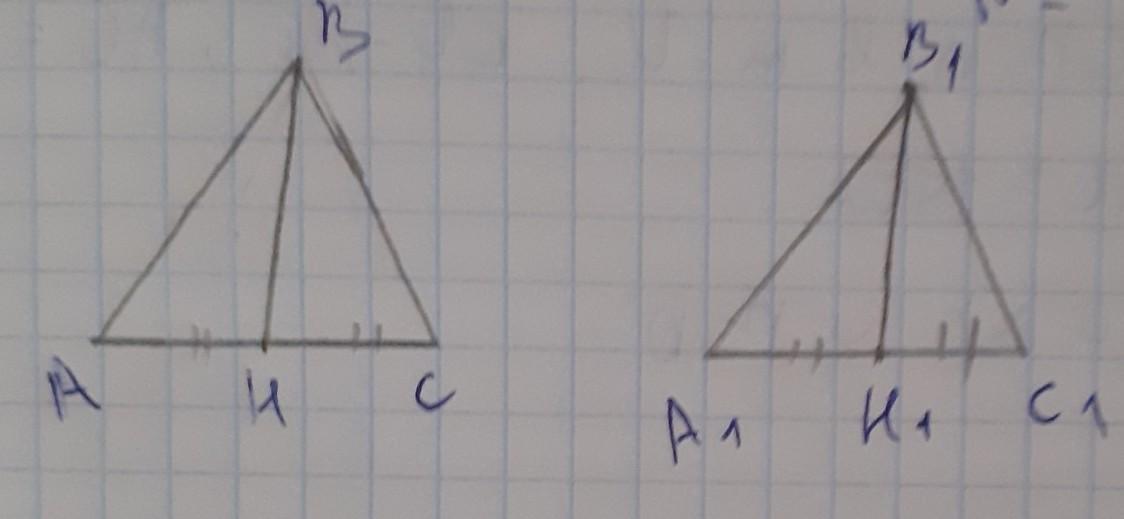
2. Даны два треугольника АВС и А1В1С1,в которых ВН и В1Н1 – соответственно их биссектрисы. Доказать равенство треугольников АВН и А1В1Н1. (7 класс)
Приложения:
Alyssa08:
Мой аккаунт Алиса Дубская
А что за ава?
У меня в статусе написан мой аккаунт в знаниях
Девочка нарисована там
Брюнетка
Понел, нашла
Это кстати, я нарисована на аватарке)
Нарисована? Я думала, что это фотография
Нет, это фотография
Я оговарилась)
Ответы
Автор ответа:
3
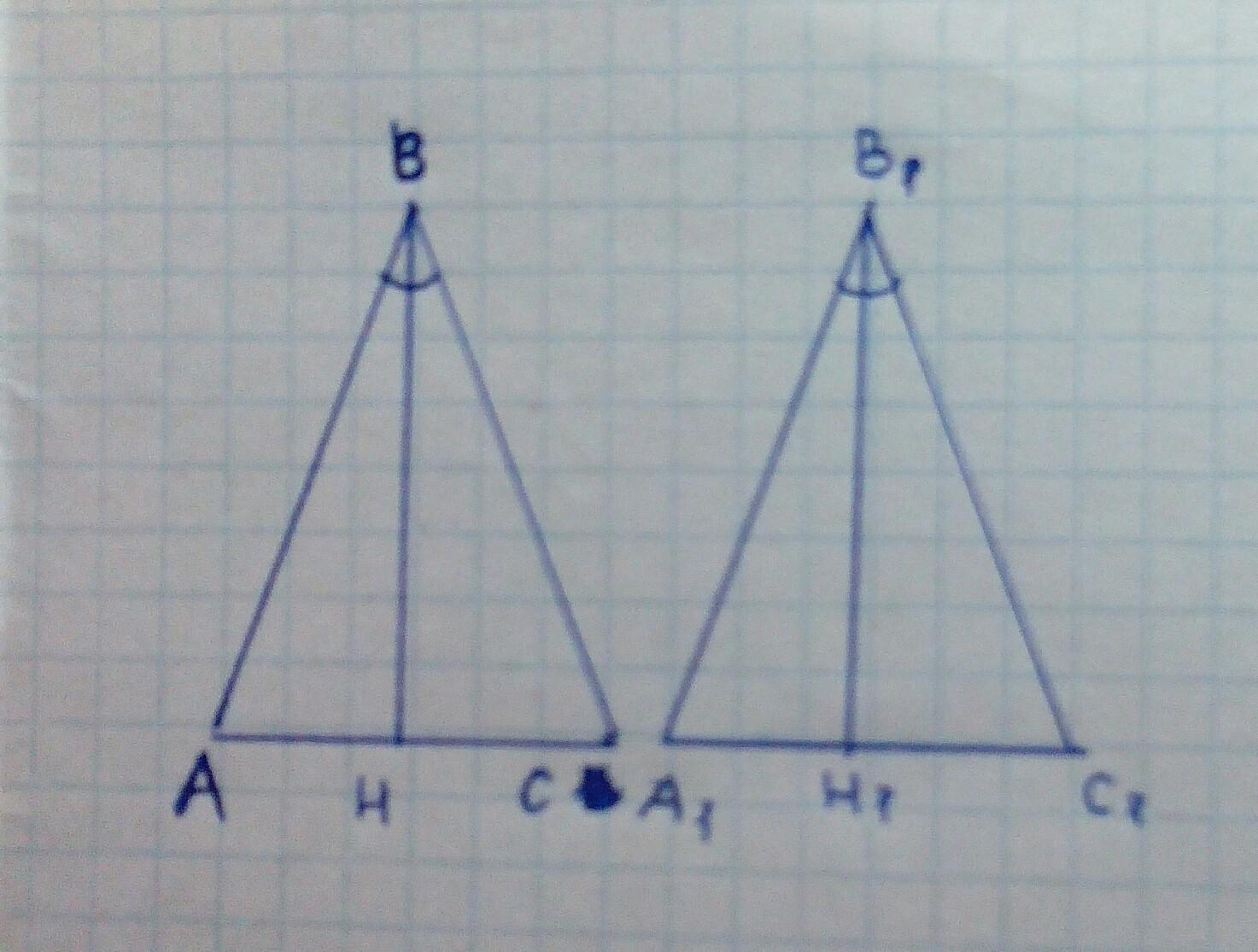
∆АВС = ∆А1В1С1 => все стороны и углы этих треугольников между собой равны.
Рассмотрим ∆АВН и ∆А1В1Н1:
АВ = А1В1, так как треугольники АВС и А1В1С1 равны
∠А = ∠А1, так как треугольники АВС и А1В1С1 равны.
Так как ВН и В1Н1 - биссектрисы и они делят углы на два равных угла, то ∠АВН = ∠А1В1Н1.
=> ∆АВН = ∆А1В1Н1, по 2 признаку равенства треугольников.
Ч.Т.Д.
Приложения:
Огромное спасибо!!!!
Спасибо за чертёж
Всё понятно?
Да. Получается, что 2 задача однотипная?
Похожие вопросы
Предмет: Русский язык,
автор: Даша123450
Предмет: Русский язык,
автор: Евгения33Мажарова
Предмет: Русский язык,
автор: ravilka74
Предмет: Математика,
автор: Serko1243