Предмет: Геометрия,
автор: annapilaer2005
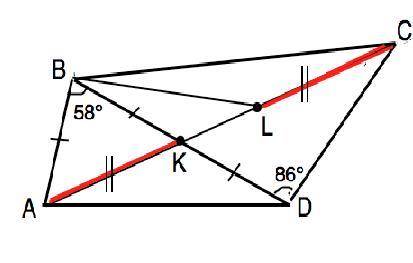
Диагонали четырёхугольника ABCDABCD пересекаются в точке KK. Оказалось, что AB=BK=KDAB=BK=KD. На отрезке KCKC отметили такую точку LL, что AK=LCAK=LC. Найдите ∠BLA∠BLA, если известно, что ∠ABD=58∘∠ABD=58∘ и ∠CDB=86∘∠CDB=86∘.
Hrisula:
Диагонали четырёхугольника ABCD пересекаются в точке K. Оказалось, что AB=BK=KD. На отрезке KC отметили такую точку L, что AK=LC. Найдите ∠BLA, если известно, что ∠ABD=58∘ и ∠CDB=86∘∘
Ответы
Автор ответа:
2
Ответ: 33°
Объяснение:∘
Сделаем рисунок согласно условию. ∆ АВК - равнобедренный, т.к.АВ=ВК (дано). ⇒ углы при основании АК равны.
Из суммы углов треугольника ∠ВАК=∠ ВКА=(180°-58°):2=61°
В ∆ ABL и ∆ CKD стороны BA=KD; отрезки AL=СL (дано); ( дано);
АК+KL =CL+KL, ⇒ AL=CK.
∠СКD=∠ВКА=61° - вертикальные.⇒
∆ ABL = ∆ CKD по 1-му признаку равенства.
Из суммы углов треугольника в ∆ КСD
∠КСD=180°-∠CKD-∠CDK=180°-61°-86°=33° ⇒
∠ВLA=∠KCD=33°
Приложения:
На странице https://znanija.com/task/36817645 в комментариях под вопросом дан другой способ решения такой задачи.
Похожие вопросы
Предмет: Русский язык,
автор: Tsuyufatboy
Предмет: Русский язык,
автор: bossmranonim
Предмет: Русский язык,
автор: ira1234567891011
Предмет: Физика,
автор: MonyRM
Предмет: Биология,
автор: ulianina2308