Предмет: Математика,
автор: DubrovskiyT
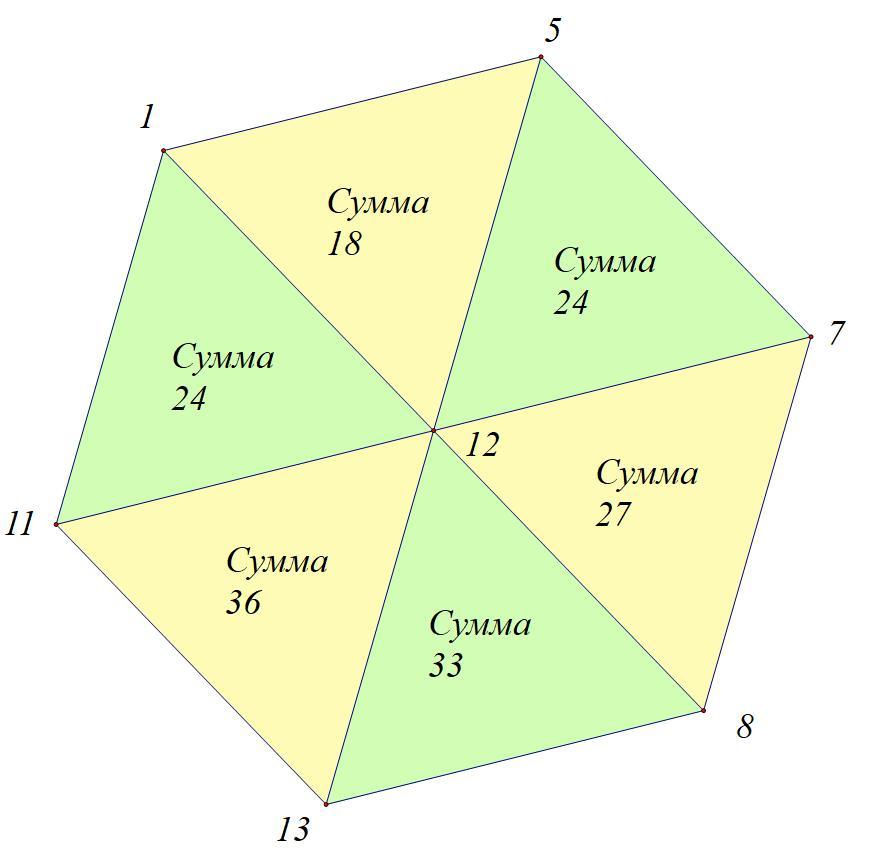
Глеб расставил числа 1, 5, 7, 8, 11, 12, 13 в вершины и центр правильного шестиугольника так, что в любом из 6 равносторонних треугольников сумма чисел в вершинах делится на 3. Какое число Глеб мог записать в центр? Достаточно привести один подходящий пример.
Ответы
Автор ответа:
3
Ответ: 12
Решение во вложении.
Как заполнялось.
Сначала произвольно ставилось число в центр.
Для начала взяли число 12, так как оно делится на 3. Значит надо расставлять по краям такие числа, чтобы при сложении соседних, получалось число, кратное 3.
Произвольно выберем вершину и поставим цифру 1. Тогда надо подобрать такое число (из имеющихся), чтобы (1 + X) делилось на 3.
1 + 5 = 6 -- делится на 3 -- подходит
Ставим число 5 около соседней вершины (решений у задачи много, поэтому может быть и другое число: 11 или 8)
Далее (5 + Х) делится на 3, откуда подходит число 7, записываем его рядом с 5. И далее аналогично:
7 + 8 = 15 -- делится,
8 + 13 = 21 -- делится,
13 + 11 = 24 -- делится,
11 + 1 = 12 -- делится.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: adamovka77
Предмет: Русский язык,
автор: дашка20032222
Предмет: Английский язык,
автор: александра1454
Предмет: История,
автор: Саняkv
Предмет: Алгебра,
автор: shefnerolga5