Question

СРОЧНО 70 БАЛЛОВ!!!!!!
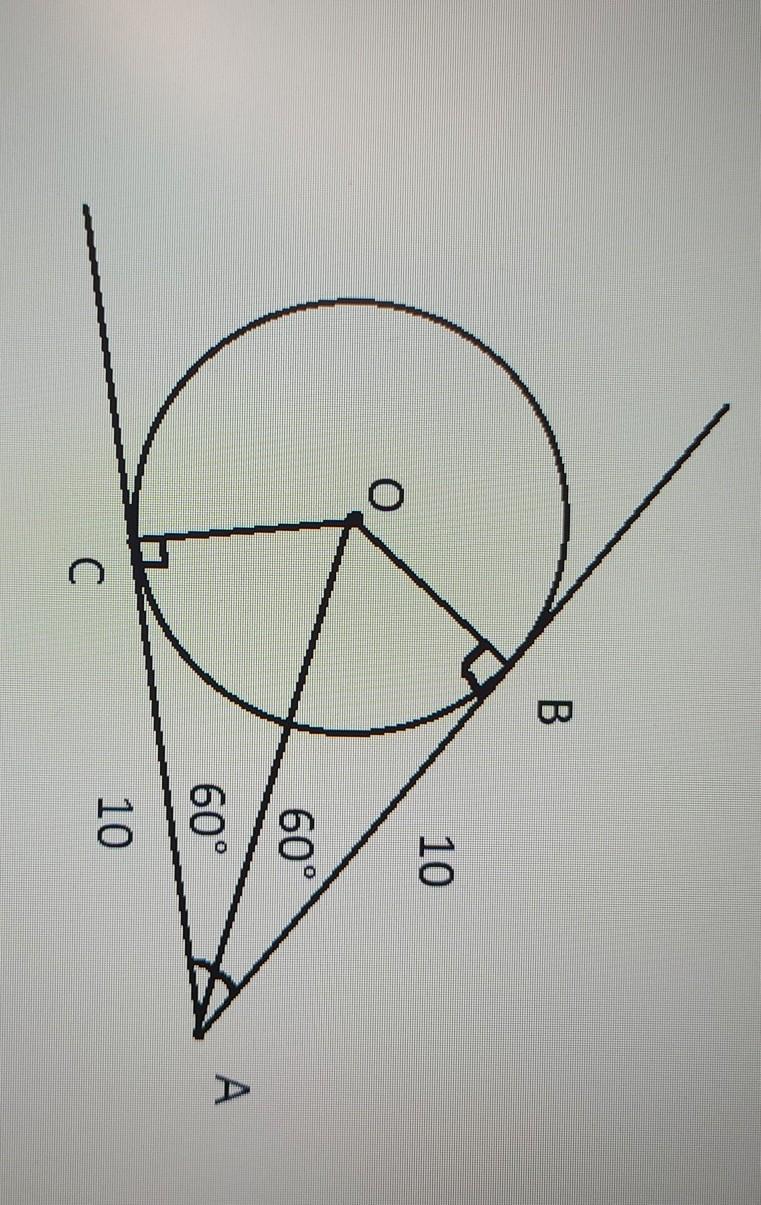
Из точки А проведены две касательные к окружности с центром в точке О. Расстояние от точки А до точки касания равно 10 см, угол между касательными равен 120°. Найти радиус окружности.

Answer 1

Если из точки А проведены две касательные к окружности с центром О, то АО - биссектриса угла А.

Если угол А = 120°, то угол ВАО = углу САО = 60°.

Радиус окружности перпендикулярен касательной. Отсюда треугольник АОВ - прямоугольный.

Если треугольник АОВ - прямоугольный и угол ОАВ = 60°, то угол ВОА = 30°.

Катет, лежащий против угла в 30°, равен половине гипотенузы. Из этого гипотенуза АО = ВА · 2 = 10 · 2 = 20 (см).

* дальше будем находить ОВ, он является как катетом, лежащим против угла в 60°, так и радиусом окружности! *

Катет, лежащий против угла 60°, равен произведению гипотенузы на sin60° => Катет, лежащий против угла 60°, равен произведению гиотенузв на √3/2.

Зная это, легко можно найти этот катет (ОВ) он равен АО · √3/2 = 20 · √3/2 = 10√3 (см).

- - - - - - - - - - - - - - - - - - - - - - - -

задача решена! можно радоваться :)