Question

Стороны параллелограмма с периметром 30 см относятся как 2 и: 3. Найдите его площадь, если острый угол параллелограмма равен 30°
а)26 см²; в)27 см²;с)29см²;d)30см²​

Answer 1

Обозначим меньшую сторону параллелограмма за a = 2х (см), тогда большую — за b = 3х (см). Составим и решим математическую модель, используя формулу периметра парал-ма:

   $2\cdot (2x+3x) = 30\\ 2\cdot 5x = 30\\ 10x = 30\\ x = 3$

Следовательно, меньшая сторона равна a = 2х = 2·3 = 6 (см), большая сторона равна b = 3х = 3·3 = 9 (cm).

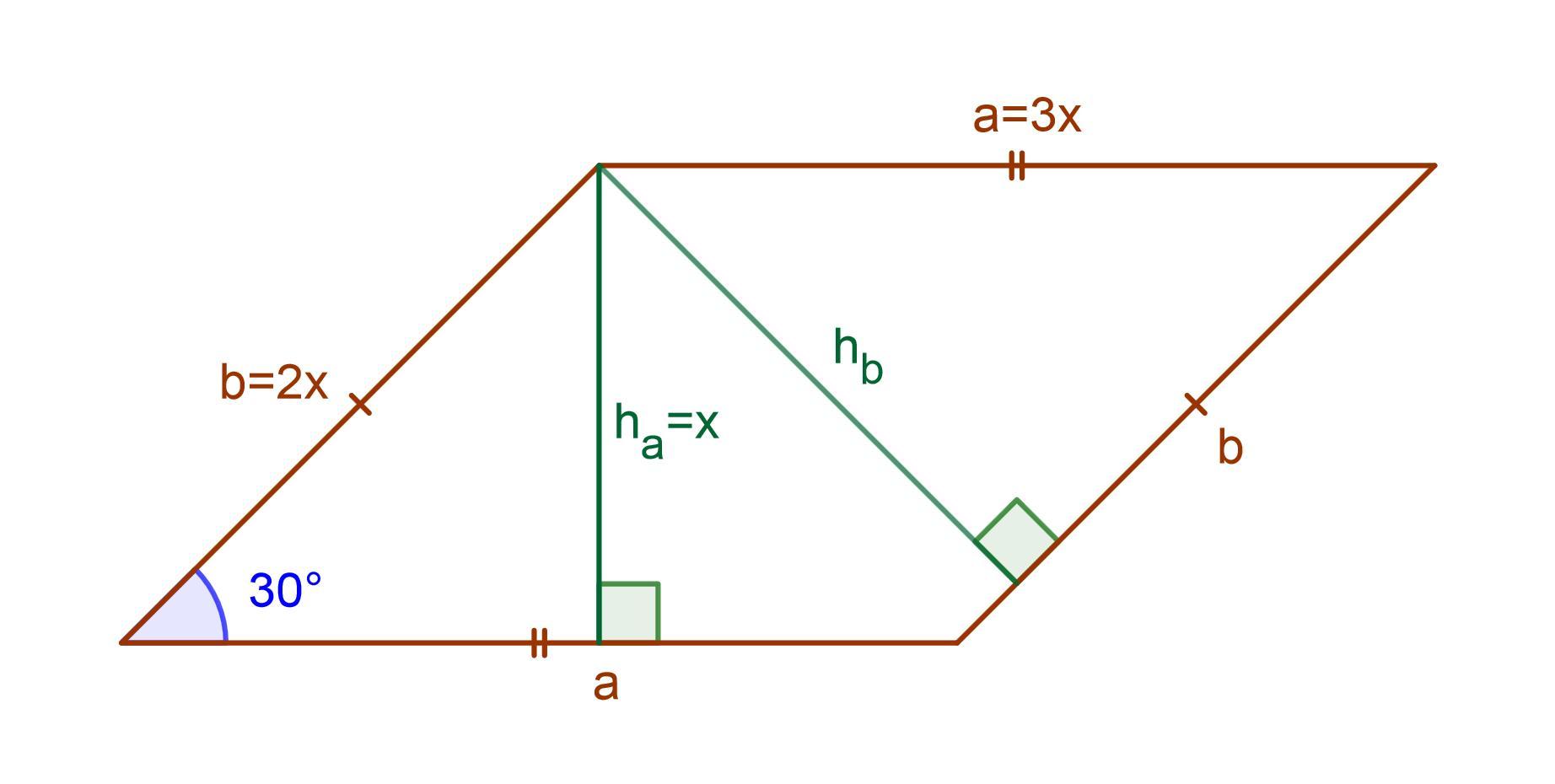
Проведем высоту hₐ из тупого угла параллелограмма на сторону a. Получим прямоугольный треугольник с катетом (высота hₐ), лежащим напротив угла 30°.

   $h_a = \frac{1}{2} b = \frac{2x}{2} = x = 3 (cm)$

Подставим значения в формулу площади параллелограмма:

   $S = ah_a\\S = 9\cdot 3 = 27 \:\: (cm^2)$

Ответ: площадь равна 27 cm².