Question

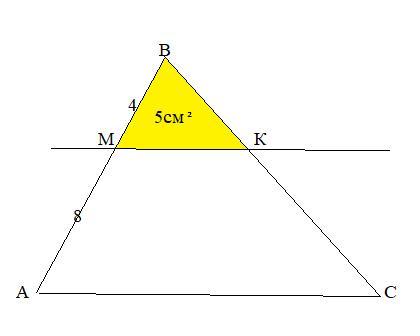
Прямая, параллельная стороне АС треугольника АВС, пересекает его сторону АВ в точке М, а сторону ВС - в точке К. Найдите площадь трапеции АМКС, если ВМ - 4 см, AM = 8 см, а треугольника МВК равна 5 см2.

Answer 1

Прямая, параллельная стороне АС треугольника АВС, пересекает его сторону АВ в точке М, а сторону ВС - в точке К. Найдите площадь трапеции АМКС, если ВМ - 4 см, AM = 8 см, а ПЛОЩАДЬ треугольника МВК равна 5 см2.

Объяснение:

АВ=4+8=12 (см).

ΔВМК подобен ΔВАС по двум углам:

∠В-общий, ∠ВМК=∠ВАС как соответственные при МК║АС, АВ-секущая. Значит сходственные стороны пропорциональны , а отношение сходственных сторон равно коэффициенту подобия:

ВМ/ВА=к , к=4/12=1/3.

Отношение площадей подобных треугольников равно к² :

S(ВМК)/S(ВАС)=к² или   5/S(ВАС)=1/9  или S(ВАС)=45 см².

S(АМКС)=S(ВАС)-S(ВМК)=45-5=40 (см²)