Предмет: Геометрия,
автор: Barbuckeri
Точка D не принадлежит плоскости
треугольника АВС. Точка D равноудалена
от концов отрезка ВС, точка А также
равноудалена от концов отрезка ВС.
Докажите, что прямые ВС и АD
перпендикулярны.
Simba2017:
АВС равнобедренный и А лежит на его высоте , значит АН(Н-середина ВС) перпендикулярна ВС
класс 10-11?
да
Ответы
Автор ответа:
4
Ответ:
Объяснение:
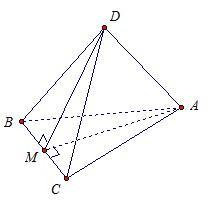
пусть М - середина отрезка BC. треугольник ABC– равнобедренный, так как АВ = АС. Тогда медиана АМ является и высотой, то есть AM перпендикулярна BC
Треугольник DВС – равнобедренный, так как DВ = DС. Тогда медиана DМ является и высотой, то есть DM перпендикулярна BC
Прямая ВС перпендикулярна двум пересекающимся прямым DM и AM из плоскости DMA, а значит, прямая ВС перпендикулярна прямой DA, которая лежит в плоскости DMA, что и требовалось доказать.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: 25021999c
Предмет: Другие предметы,
автор: shamil99fd
Предмет: Русский язык,
автор: Lizok585
Предмет: Алгебра,
автор: JABKANO
Предмет: Математика,
автор: Аноним