Предмет: Алгебра,
автор: denislotar
Найти следующие пределы
Приложения:
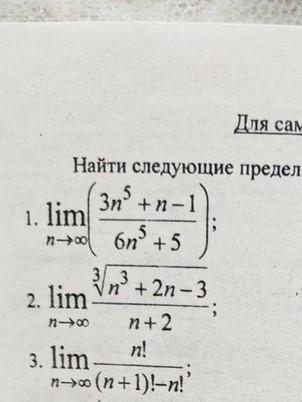
Ответы
Автор ответа:
0
1klass051:
Привет всем помогите мне пожалуйста с математикой
Похожие вопросы
Предмет: Алгебра,
автор: Аноним
Предмет: Математика,
автор: kgn345
Предмет: Алгебра,
автор: параня1956
Предмет: История,
автор: яно001
Предмет: Литература,
автор: xzkakoynik