Предмет: Алгебра,
автор: vitja037
Помогите небольшие 2 задания, с обьяснением
27 и 28
Приложения:
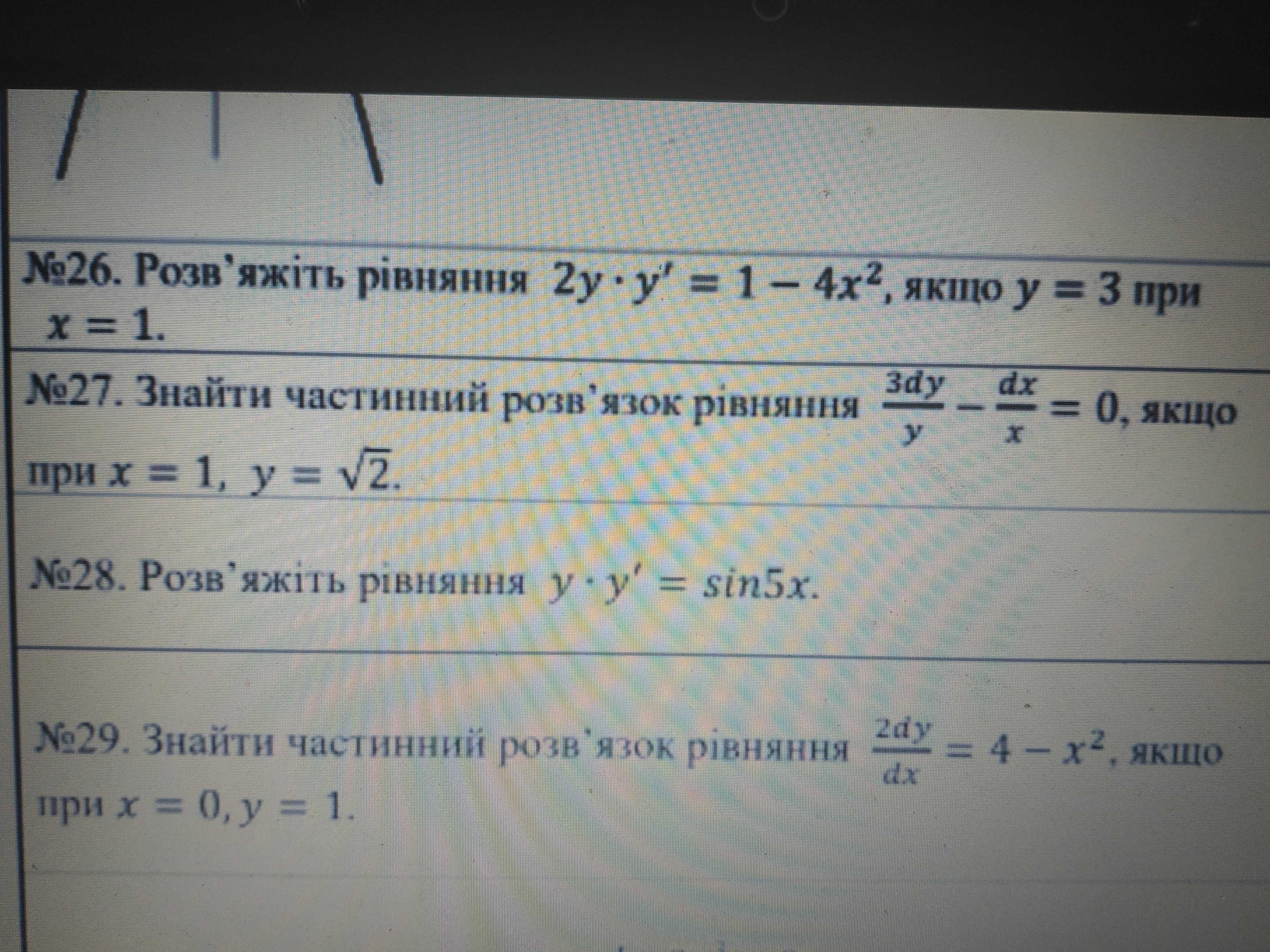
Ответы
Автор ответа:
1
bsggv6:
Здравствуйте можете мне помочь с математикой прошу вас
Похожие вопросы
Предмет: Русский язык,
автор: веран
Предмет: Математика,
автор: илья1802
Предмет: Математика,
автор: Nataliportman
Предмет: Химия,
автор: Юлия1234321
Предмет: География,
автор: ghghtAnelbh6f