Предмет: Геометрия,
автор: lysenk000
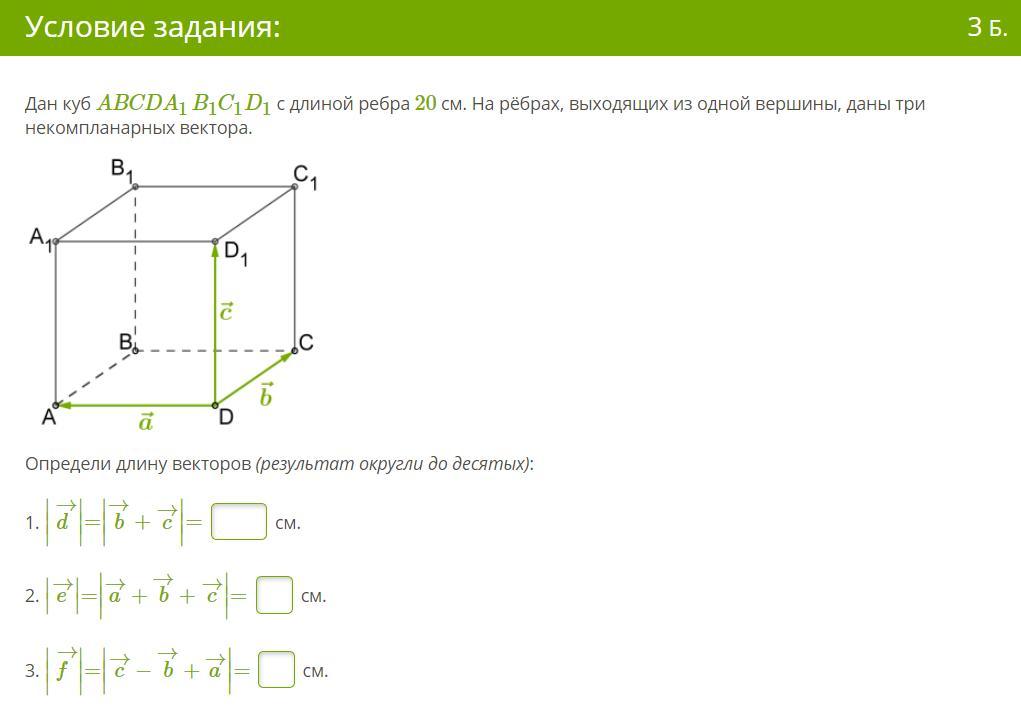
пожалуйста 70 баллов Дан куб ABCDA1B1C1D1 с длиной ребра 20 см. На рёбрах, выходящих из одной вершины, даны три некомпланарных вектора.
Определи длину векторов (результат округли до десятых):
Приложения:
Ответы
Автор ответа:
4
1) По правилу параллелограмма, если векторы имеют общее начало, то сумма векторов - это вектор, равный диагонали параллелограмма, начало которой в той же точке, что и начала векторов-слагаемых.
см .
см.
см.
Похожие вопросы
Предмет: Алгебра,
автор: vinyaikina
Предмет: Математика,
автор: 123456м
Предмет: Обществознание,
автор: buchneva1994
Предмет: Литература,
автор: pnurkhonova55
Предмет: Математика,
автор: daryameduyants