Предмет: Геометрия,
автор: lubachebotkova
У рівнобедрений трикутник вписано коло, яке ділить бічну
сторону у відношенні 2:3, починаючи від вершини, що лежить
навпроти основи. Знайдіть сторони трикутника, якщо
периметр трикутника дорівнює 320 см.
Ответы
Автор ответа:
23
Ответ:
100,100;120
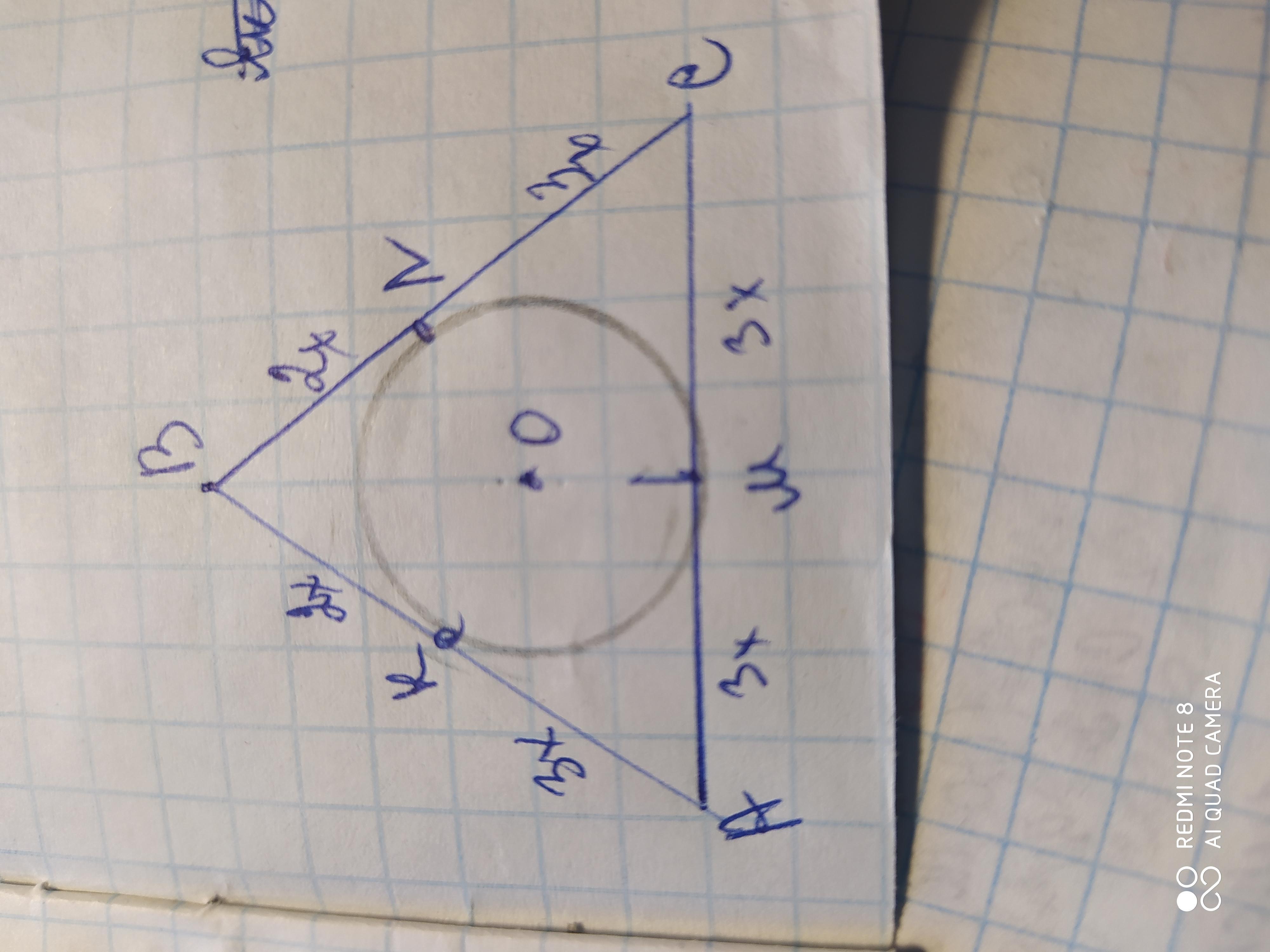
Объяснение: Якщо ΔАВС - рівнобедрений, АВ=ВС.
З умови ВК:КВ=2:3, тоді ВК=2х, КА=3х, а АВ=ВС=5х
АМ=МС(т.М - точка дотику лежить на бісекртрисі( і медіані у рівнобедреному тр-ку)
АМ=АК=3х( як відрізки двох дтичних)⇒АС=2×3х=6х
РΔ=АВ+ВС+СА=5х+5х+6х=16х
16х=320
х=20
АВ=ВС=5х= 5×20=100см
АС=6х=6×20=120см
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: rufataliev76
Предмет: Химия,
автор: Katusha0987
Предмет: Химия,
автор: alena2505
Предмет: Математика,
автор: sergejbaev03